We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We give a simple argument which shows that Gabor systems consisting of oddfunctions of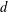 
$d$ variables and symplectic lattices of density 
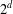$2^{d}$ cannot constitute a Gabor frame. In the one-dimensional,separable case, this follows from a more general result of Lyubarskii andNes [‘Gabor frames with rational density’, Appl. Comput. Harmon. Anal.34(3) (2013), 488–494]. We use a differentapproach exploiting the algebraic relation between the ambiguity functionand the Wigner distribution as well as their relation given by the(symplectic) Fourier transform. Also, we do not need the assumption that thelattice is separable and, hence, new restrictions are added to the fullframe set of odd functions.
