We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Let J(m) be an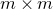 
$m\times m$ Jordan block with eigenvalue 1. For 
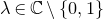$\lambda\in\mathbb{C}\setminus\{0,1\}$, we explicitly construct all rank 2 local systems of geometric origin on 
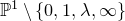$\mathbb{P}^1\setminus\{0,1,\lambda,\infty\}$, with local monodromy conjugate to J(2) at 
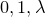$0,1,\lambda$ and conjugate to 
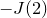$-J(2)$ at 
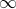$\infty$. The construction relies crucially on Katz’s middle convolution operation. We use our construction to prove two conjectures of Sun, Yang and Zuo (one of which was proven earlier by Lin, Sheng and Wang; the other was proven independently of us by Yang and Zuo) coming from the theory of Higgs–de Rham flows, as well as a special case of the periodic Higgs conjecture of Krishnamoorthy and Sheng.
