We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
It is proven that a matched pair of actions on a Hopf algebra H is equivalent to the datum of a Yetter–Drinfeld brace, which is a novel structure generalizing Hopf braces. This [-30pt] improves a theorem by Angiono, Galindo, and Vendramin, originally stated for cocommutative Hopf braces. These Yetter–Drinfeld braces produce Hopf algebras in the category of Yetter–Drinfeld modules over H, through an operation that generalizes Majid’s transmutation. A characterization of Yetter–Drinfeld braces via 1-cocycles, in analogy to the one for Hopf braces, is given.
Every coquasitriangular Hopf algebra H will be seen to yield a Yetter–Drinfeld brace, where the additional structure on H is given by the transmutation. We compute explicit examples of Yetter–Drinfeld braces on the Sweedler’s Hopf algebra, on the algebras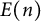 
$E(n)$, on 
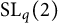$\mathrm {SL}_{q}(2)$, and an example in the class of Suzuki algebras.
