We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
For a continuous and positive function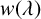 
$w(\lambda )$, 
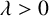$\lambda>0$ and 
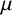$\mu $ a positive measure on 
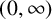$(0,\infty )$, we consider the integral transform 
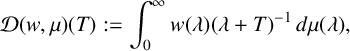$$ \begin{align*} \mathcal{D}( w,\mu ) ( T) :=\int_{0}^{\infty }w(\lambda) ( \lambda +T) ^{-1}\,d\mu ( \lambda ) , \end{align*} $$
where the integral is assumed to exist for T a positive operator on a complex Hilbert space H. We show among other things that if B,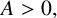 
$A>0,$ then 
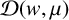$\mathcal {D}( w,\mu ) $ is operator subadditive on 
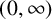$(0,\infty ) $, that is, 
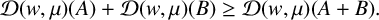$$ \begin{align*} \mathcal{D}( w,\mu ) ( A) +\mathcal{D}( w,\mu) ( B) \geq \mathcal{D}( w,\mu )(A+B). \end{align*} $$
From this, we derive that if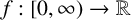 
$f:[0,\infty )\rightarrow \mathbb {R}$ is an operator monotone function on 
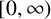$[0,\infty )$, then the function 
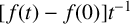$[ f( t) -f( 0) ] t^{-1}$ is operator subadditive on 
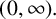$( 0,\infty ) .$ Also, if 
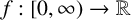$f:[0,\infty )\rightarrow \mathbb {R}$ is an operator convex function on 
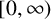$[0,\infty )$, then the function 
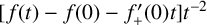$[ f( t) -f( 0) -f_{+}^{\prime }( 0) t ] t^{-2}$ is operator subadditive on 
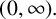$( 0,\infty ) .$
