We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
The process generated by the crossings of a fixed level, u, by the process Pn (t) is considered, where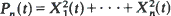
and the Xi (t) are identical, independent, separable, stationary, zero mean, Gaussian processes. A simple formula is obtained for the expected number of upcrossings in a given time interval, sufficient conditions are given for the upcrossings process to tend to a Poisson process as u→∞, and it is shown that under suitable scaling the distribution of the length of an excursion of Pn (t) above u tends to a Rayleigh distribution as u→ ∞.
