A ring R has right property (A) whenever a finitely generated two-sided ideal of R consisting entirely of left zero-divisors has a non-zero right annihilator. As the main result of this paper we give answers to two questions related to property (A), raised by Hong et al. One of the questions has a positive answer and we obtain it as a simple conclusion of the fact that if R is a right duo ring and M is a u.p.-monoid (unique product monoid), then R is right M-McCoy and the monoid ring R[M] has right property (A). The second question has a negative answer and we demonstrate this by constructing a suitable example.

Let $R$ be an associative ring with identity. First we prove some results about zero-divisor graphs of reversible rings. Then we study the zero-divisors of the skew power series ring 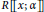$R\left[\!\left[ x;\,\alpha\right]\!\right]$ , whenever $R$ is reversible $\alpha$ -compatible. Moreover, we compare the diameter and girth of the zero-divisor graphs of 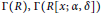$\Gamma \left( R \right),\,\Gamma \left( R[x;\,\alpha ,\,\delta ] \right)$ , and 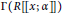$\Gamma \left( R\left[\!\left[ x;\,\alpha\right]\!\right] \right)$ , when $R$ is reversible and 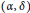$\left( \alpha ,\,\delta\right)$ -compatible.