We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
In this paper, we consider a notion of nonmeasurablity with respect to Marczewski and Marczewski-like tree ideals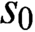 
$s_0$, 
$m_0$,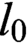 
$l_0$, 
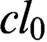$cl_0$, 
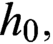$h_0,$ and 
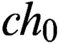$ch_0$. We show that there exists a subset of the Baire space 
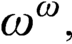$\omega ^\omega ,$ which is s-, l-, and m-nonmeasurable that forms a dominating m.e.d. family. We investigate a notion of 
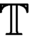${\mathbb {T}}$-Bernstein sets—sets which intersect but do not contain any body of any tree from a given family of trees 
${\mathbb {T}}$. We also obtain a result on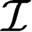 
${\mathcal {I}}$-Luzin sets, namely, we prove that if 
${\mathfrak {c}}$ is a regular cardinal, then the algebraic sum (considered on the real line 
${\mathbb {R}}$) of a generalized Luzin set and a generalized Sierpiński set belongs to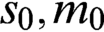 
$s_0, m_0$, 
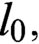$l_0,$ and 
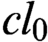$cl_0$.
