Refine search
Actions for selected content:
3 results
22 - Conclusion
- from Part V - The Long-Term Goal: Envisioning a Mature System of Global Governance for the Twenty-Second Century
-
- Book:
- Planet in Peril
- Published online:
- 13 October 2022
- Print publication:
- 13 October 2022, pp 324-328
-
- Chapter
- Export citation
High efficiency second harmonic generation of nanojoule-level femtosecond pulses in the visible based on BiBO
-
- Journal:
- High Power Laser Science and Engineering / Volume 7 / 2019
- Published online by Cambridge University Press:
- 14 February 2019, e11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Limit Theorems for Moving Averages with Random Coefficients and Heavy-Tailed Noise
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 1 / March 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 245-256
- Print publication:
- March 2006
-
- Article
-
- You have access
- Export citation
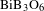
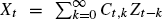 , generated by an array, {
, generated by an array, {