We consider the following semilinear elliptic equation:

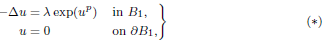
where B 1 is the unit ball in ℝd , d ≥ 3, λ > 0 and p > 0. Firstly, following Merle and Peletier, we show that there exists an eigenvalue λ p,∞ such that (*) has a solution (λ p,∞ ,W p ) satisfying lim|x|→0 Wp (x) = ∞. Secondly, we study a bifurcation diagram of regular solutions to (*). It follows from the result of Dancer that (*) has an unbounded bifurcation branch of regular solutions that emanates from (λ, u) = (0, 0). Here, using the singular solution, we show that the bifurcation branch has infinitely many turning points around λp,∞ when 3 ≤ d ≤ 9. We also investigate the Morse index of the singular solution in the d ≥ 11 case.

We study the periodic and Neumann boundary-value problems associated with the second-order nonlinear differential equation

where is a sublinear function at infinity having superlinear growth at zero. We prove the existence of two positive solutions when

and λ > 0 is sufficiently large. Our approach is based on Mawhin's coincidence degree theory and index computations.

Motivated by some non-local boundary-value problems (BVPs) that arise in heat-flow problems, we establish new results for the existence of non-zero solutions of integral equations of the form

$$ u(t)=\gamma(t)\alpha[u]+\int_{G}k(t,s)f(s,u(s))\,\mathrm{d}s, $$

where $G$ is a compact set in $\mathbb{R}^{n}$. Here $\alpha[u]$ is a positive functional and $f$ is positive, while $k$ and $\gamma$ may change sign, so positive solutions need not exist. We prove the existence of multiple non-zero solutions of the BVPs under suitable conditions. We show that solutions of the BVPs lose positivity as a parameter decreases. For a certain parameter range not all solutions can be positive, but for one of the boundary conditions we consider we show that there are positive solutions for certain types of nonlinearity. We also prove a uniqueness result.