We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
The present paper considers the stochastic difference equation Y n = A n Y n-1 + B n with i.i.d. random pairs (A n , B n ) and obtains conditions under which Y n converges in distribution. This convergence is related to the existence of solutions of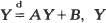 
and (A, B) independent, and the convergence w.p. 1 of ∑ A 1 A 2 ··· A n-1 B n . A second subject is the series ∑ C n f(T n ) with (C n ) a sequence of i.i.d. random variables, (T n ) the sequence of points of a Poisson process and f a Borel function on (0, ∞). The resulting random variable turns out to be infinitely divisible, and its Lévy–Hinčin representation is obtained. The two subjects coincide in case A n and C n are independent, B n = A n C n , A n = U 1/α n with U n a uniform random variable, f(x) = e −x/α.
