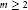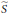Refine search
Actions for selected content:
8 results
Chapter 3 - Germany
- from Part I - Places
-
-
- Book:
- Pirandello in Context
- Published online:
- 14 March 2024
- Print publication:
- 21 March 2024, pp 18-26
-
- Chapter
- Export citation

Hitler's Panzer Generals
- Guderian, Hoepner, Reinhardt and Schmidt Unguarded
-
- Published online:
- 04 May 2023
- Print publication:
- 04 May 2023
2 - The Private Generals
-
- Book:
- Hitler's Panzer Generals
- Published online:
- 04 May 2023
- Print publication:
- 04 May 2023, pp 22-74
-
- Chapter
- Export citation
1 - The Letters of the Panzer Generals
-
- Book:
- Hitler's Panzer Generals
- Published online:
- 04 May 2023
- Print publication:
- 04 May 2023, pp 10-21
-
- Chapter
- Export citation
4 - The Criminal Generals
-
- Book:
- Hitler's Panzer Generals
- Published online:
- 04 May 2023
- Print publication:
- 04 May 2023, pp 133-182
-
- Chapter
- Export citation
3 - The Public Generals
-
- Book:
- Hitler's Panzer Generals
- Published online:
- 04 May 2023
- Print publication:
- 04 May 2023, pp 75-132
-
- Chapter
- Export citation
5 - The Military Generals
-
- Book:
- Hitler's Panzer Generals
- Published online:
- 04 May 2023
- Print publication:
- 04 May 2023, pp 183-238
-
- Chapter
- Export citation
On Certain Multivariable Subnormal Weighted Shifts and their Duals
-
- Journal:
- Canadian Mathematical Bulletin / Volume 56 / Issue 3 / 01 September 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 459-465
- Print publication:
- 01 September 2013
-
- Article
-
- You have access
- Export citation