Assume a point $z$ lies in the open unit disk $\mathbb{D}$ of the complex plane $\mathbb{C}$ and $f$ is an analytic self-map of $\mathbb{D}$ fixing 0. Then Schwarz’s lemma gives $|f(z)|\leq |z|$, and Dieudonné’s lemma asserts that $|f^{\prime }(z)|\leq \min \{1,(1+|z|^{2})/(4|z|(1-|z|^{2}))\}$. We prove a sharp upper bound for $|f^{\prime \prime }(z)|$ depending only on $|z|$.

Let ${\mathcal{S}}$ be the family of analytic and univalent functions $f$ in the unit disk $\mathbb{D}$ with the normalization $f(0)=f^{\prime }(0)-1=0$, and let $\unicode[STIX]{x1D6FE}_{n}(f)=\unicode[STIX]{x1D6FE}_{n}$ denote the logarithmic coefficients of $f\in {\mathcal{S}}$. In this paper we study bounds for the logarithmic coefficients for certain subfamilies of univalent functions. Also, we consider the families ${\mathcal{F}}(c)$ and ${\mathcal{G}}(c)$ of functions $f\in {\mathcal{S}}$ defined by

$$\begin{eqnarray}\text{Re}\biggl(1+{\displaystyle \frac{zf^{\prime \prime }(z)}{f^{\prime }(z)}}\biggr)>1-{\displaystyle \frac{c}{2}}\quad \text{and}\quad \text{Re}\biggl(1+{\displaystyle \frac{zf^{\prime \prime }(z)}{f^{\prime }(z)}}\biggr)<1+{\displaystyle \frac{c}{2}},\quad z\in \mathbb{D},\end{eqnarray}$$

$c\in (0,3]$

$c\in (0,1]$

$|\unicode[STIX]{x1D6FE}_{n}|$

$n=1,2,3$

$f$

${\mathcal{F}}(c)$

${\mathcal{G}}(c)$

• ∙ If $f\in {\mathcal{F}}(-1/2)$, then $|\unicode[STIX]{x1D6FE}_{n}|\leq 1/n(1-(1/2^{n+1}))$ for $n\geq 1$, and

  $$\begin{eqnarray}\mathop{\sum }_{n=1}^{\infty }|\unicode[STIX]{x1D6FE}_{n}|^{2}\leq {\displaystyle \frac{\unicode[STIX]{x1D70B}^{2}}{6}}+{\displaystyle \frac{1}{4}}~\text{Li}_{2}\biggl({\displaystyle \frac{1}{4}}\biggr)-\text{Li}_{2}\biggl({\displaystyle \frac{1}{2}}\biggr),\end{eqnarray}$$
  where $\text{Li}_{2}(x)$ denotes the dilogarithm function.

• ∙ If $f\in {\mathcal{G}}(c)$, then $|\unicode[STIX]{x1D6FE}_{n}|\leq c/2n(n+1)$ for $n\geq 1$.

Let 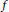$f$ be a holomorphic function of the unit disc 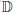$\mathbb{D}$ , preserving the origin. According to Schwarz’s Lemma, 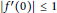$\left| {{f}^{\prime }}(0) \right|\,\le \,1$ , provided that 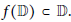$f(\mathbb{D})\,\subset \,\mathbb{D}$ . We prove that this bound still holds, assuming only that 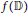$f(\mathbb{D})$ does not contain any closed rectilinear segment 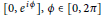$\left[ 0,\,{{e}^{i\phi }} \right],\,\phi \,\in \,\left[ 0,\,2\pi\right]$ , i.e., does not contain any entire radius of the closed unit disc. Furthermore, we apply this result to the hyperbolic density and give a covering theorem.

For holomorphic functions $f$ in the unit disk $ \mathbb{D} $ with $f(0)= 0$, we prove a modulus growth bound involving the logarithmic capacity (transfinite diameter) of the image. We show that the pertinent extremal functions map the unit disk conformally onto the interior of an ellipse. We prove a modulus growth bound for elliptically schlicht functions in terms of the elliptic capacity ${\mathrm{d} }_{\mathrm{e} } f( \mathbb{D} )$ of the image. We also show that the function ${\mathrm{d} }_{\mathrm{e} } f(r \mathbb{D} )/ r$ is increasing for $0\lt r\lt 1$.