We almost completely solve a number of problems related to a concept called majority colouring recently studied by Kreutzer, Oum, Seymour, van der Zypen and Wood. They raised the problem of determining, for a natural number k, the smallest number m = m(k) such that every digraph can be coloured with m colours where each vertex has the same colour as at most a 1/k proportion of its out-neighbours. We show that m(k) ∈ {2k − 1,2k}. We also prove a result supporting the conjecture that m(2) = 3. Moreover, we prove similar results for a more general concept called majority choosability.

Let Dk denote the tournament on 3k vertices consisting of three disjoint vertex classes V 1, V 2 and V 3 of size k, each oriented as a transitive subtournament, and with edges directed from V 1 to V 2, from V 2 to V 3 and from V 3 to V 1. Fox and Sudakov proved that given a natural number k and ε > 0, there is n 0(k, ε) such that every tournament of order n ⩾ n 0(k,ε) which is ε-far from being transitive contains Dk as a subtournament. Their proof showed that 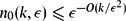$n_0(k,\epsilon ) \leq \epsilon ^{-O(k/\epsilon ^2)}$ and they conjectured that this could be reduced to n 0(k, ε) ⩽ ε−O(k). Here we prove this conjecture.

One of the first graph-theoretical problems to be given serious attention (in the 1950s) was the decision whether a given integer sequence is equal to the degree sequence of a simple graph (or graphical, for short). One method to solve this problem is the greedy algorithm of Havel and Hakimi, which is based on the swap operation. Another, closely related question is to find a sequence of swap operations to transform one graphical realization into another of the same degree sequence. This latter problem has received particular attention in the context of rapidly mixing Markov chain approaches to uniform sampling of all possible realizations of a given degree sequence. (This becomes a matter of interest in the context of the study of large social networks, for example.) Previously there were only crude upper bounds on the shortest possible length of such swap sequences between two realizations. In this paper we develop formulae (Gallai-type identities) for the swap-distances of any two realizations of simple undirected or directed degree sequences. These identities considerably improve the known upper bounds on the swap-distances.