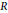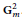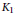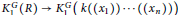Refine search
Actions for selected content:
6 results
Corrigendum: A certain structure of Artin groups and the isomorphism conjecture
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 23 February 2024, pp. 729-730
- Print publication:
- April 2024
-
- Article
-
- You have access
- HTML
- Export citation
A certain structure of Artin groups and the isomorphism conjecture
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 21 May 2020, pp. 1153-1170
- Print publication:
- August 2021
-
- Article
- Export citation
Non-stable K1-functors of Multiloop Groups
-
- Journal:
- Canadian Journal of Mathematics / Volume 68 / Issue 1 / 01 February 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 150-178
- Print publication:
- 01 February 2016
-
- Article
-
- You have access
- Export citation
Homotopy invariance of non-stable K1-functors
-
- Journal:
- Journal of K-Theory / Volume 13 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 10 October 2013, pp. 199-248
- Print publication:
- April 2014
-
- Article
- Export citation
The Farrell-Jones isomorphism conjecture for 3-manifold groups
-
- Journal:
- Journal of K-Theory / Volume 1 / Issue 1 / February 2008
- Published online by Cambridge University Press:
- 30 November 2007, pp. 49-82
- Print publication:
- February 2008
-
- Article
- Export citation
K-Theory of Solvable Groups
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 87 / Issue 2 / September 2003
- Published online by Cambridge University Press:
- 01 October 2003, pp. 309-336
- Print publication:
- September 2003
-
- Article
- Export citation