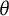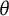In item response theory (IRT), the conventional latent trait scale (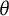$\theta $) is inherently arbitrary, lacking a fixed unit or origin and often tied to specific population distributional assumptions (e.g., standard normal). This limits the direct comparability and interpretability of scores across different tests, populations, or model estimation methods. This article introduces the “bit scale,” a novel metric transformation for unidimensional IRT scores derived from fundamental principles of information theory, specifically surprisal and entropy. Bit scores are anchored to the properties of the test items rather than the test-taker population. This item-based anchoring ensures the scale’s invariance to population assumptions and provides a consistent metric for comparing latent trait levels. We illustrate the utility of the bit scale through empirical examples: demonstrating consistent scoring when fitting models with different 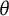$\theta $ scale assumptions, and using anchor items to directly link scores from different test administrations. A simulation study confirms the desirable statistical properties (low bias and accurate standard errors) of Maximum Likelihood-estimated bit scores and their robustness to extreme scores. The bit scale offers a theoretically grounded, interpretable, and comparable metric for reporting and analyzing IRT-based assessment results. Software implementations in R (bitscale) and Python (IRTorch) are available and practical implications are discussed.