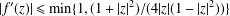Refine search
Actions for selected content:
3 results
Isometric dilation and Sarason’s commutant lifting theorem in several variables
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 25 February 2025, pp. 1-33
-
- Article
- Export citation
Refined Bohr inequalities for certain classes of functions: analytic, univalent, and convex
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 09 June 2023, pp. 9-25
- Print publication:
- March 2024
-
- Article
- Export citation
ESTIMATES OF THE SECOND DERIVATIVE OF BOUNDED ANALYTIC FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 3 / December 2019
- Published online by Cambridge University Press:
- 03 June 2019, pp. 458-469
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation