Refine search
Actions for selected content:
25 results
8 - Graph Theory, Combinatorial Optimization, and Supply Chains
-
- Book:
- Insight-Driven Problem Solving
- Published online:
- 21 October 2025
- Print publication:
- 30 October 2025, pp 250-278
-
- Chapter
- Export citation
Large language models for combinatorial optimization of design structure matrix
-
- Journal:
- Proceedings of the Design Society / Volume 5 / August 2025
- Published online by Cambridge University Press:
- 27 August 2025, pp. 2201-2210
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An Interactive Multiobjective Programming Approach to Combinatorial Data Analysis
-
- Journal:
- Psychometrika / Volume 66 / Issue 1 / March 2001
- Published online by Cambridge University Press:
- 01 January 2025, pp. 5-24
-
- Article
- Export citation
Uniform Test Assembly
-
- Journal:
- Psychometrika / Volume 73 / Issue 1 / March 2008
- Published online by Cambridge University Press:
- 01 January 2025, pp. 21-38
-
- Article
- Export citation
A Simulated Annealing Methodology for Clusterwise Linear Regression
-
- Journal:
- Psychometrika / Volume 54 / Issue 4 / December 1989
- Published online by Cambridge University Press:
- 01 January 2025, pp. 707-736
-
- Article
- Export citation
Indclus: An Individual differences Generalization of the Adclus Model and the Mapclus Algorithm
-
- Journal:
- Psychometrika / Volume 48 / Issue 2 / June 1983
- Published online by Cambridge University Press:
- 01 January 2025, pp. 157-169
-
- Article
- Export citation
Variable Neighborhood Search Heuristics for Selecting a Subset of Variables in Principal Component Analysis
-
- Journal:
- Psychometrika / Volume 74 / Issue 4 / December 2009
- Published online by Cambridge University Press:
- 01 January 2025, pp. 705-726
-
- Article
- Export citation
A Branch-and-Bound Algorithm for Fitting Anti-Robinson Structures to Symmetric Dissimilarity Matrices
-
- Journal:
- Psychometrika / Volume 67 / Issue 3 / September 2002
- Published online by Cambridge University Press:
- 01 January 2025, pp. 459-471
-
- Article
- Export citation
Matrix Reorganization and Dynamic Programming: Applications to Paired Comparisons and Unidimensional Seriation
-
- Journal:
- Psychometrika / Volume 46 / Issue 4 / December 1981
- Published online by Cambridge University Press:
- 01 January 2025, pp. 429-441
-
- Article
- Export citation
Payments under the Average Crop Revenue Program: Implications for Government Costs and Producer Preferences
-
- Journal:
- Agricultural and Resource Economics Review / Volume 38 / Issue 1 / April 2009
- Published online by Cambridge University Press:
- 15 September 2016, pp. 49-64
-
- Article
- Export citation
Efficient Convex Optimization Approaches to Variational Image Fusion
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 7 / Issue 2 / May 2014
- Published online by Cambridge University Press:
- 28 May 2015, pp. 234-250
- Print publication:
- May 2014
-
- Article
- Export citation
Analysis of a near-metric TSP approximation algorithm∗
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 47 / Issue 3 / July 2013
- Published online by Cambridge University Press:
- 06 August 2013, pp. 293-314
- Print publication:
- July 2013
-
- Article
- Export citation
Solving the Minimum Independent Domination Set Problem inGraphs by Exact Algorithm and Greedy Heuristic∗
-
- Journal:
- RAIRO - Operations Research / Volume 47 / Issue 3 / July 2013
- Published online by Cambridge University Press:
- 02 May 2013, pp. 199-221
- Print publication:
- July 2013
-
- Article
- Export citation
Scheduling an interval ordered precedence graph with communication delaysand a limited number of processors
-
- Journal:
- RAIRO - Operations Research / Volume 47 / Issue 1 / January 2013
- Published online by Cambridge University Press:
- 07 March 2013, pp. 73-87
- Print publication:
- January 2013
-
- Article
- Export citation
Minmax regret combinatorial optimization problems: an AlgorithmicPerspective
-
- Journal:
- RAIRO - Operations Research / Volume 45 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 24 August 2011, pp. 101-129
- Print publication:
- April 2011
-
- Article
- Export citation
An introduction to quantum annealing
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 45 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 15 March 2011, pp. 99-116
- Print publication:
- January 2011
-
- Article
- Export citation
Greedy algorithms for optimal computing of matrix chain products involving square denseand triangular matrices
-
- Journal:
- RAIRO - Operations Research / Volume 45 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 14 March 2011, pp. 1-16
- Print publication:
- January 2011
-
- Article
- Export citation
Quadratic 0–1 programming: Tightening linear or quadratic convex reformulation by use of relaxations
-
- Journal:
- RAIRO - Operations Research / Volume 42 / Issue 2 / April 2008
- Published online by Cambridge University Press:
- 17 May 2008, pp. 103-121
- Print publication:
- April 2008
-
- Article
- Export citation
Large neighborhood improvementsfor solving car sequencing problems
-
- Journal:
- RAIRO - Operations Research / Volume 40 / Issue 4 / October 2006
- Published online by Cambridge University Press:
- 14 February 2007, pp. 355-379
- Print publication:
- October 2006
-
- Article
- Export citation
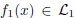 and
and 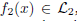 where
where 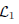 and
and 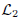 are the sets of linearly-ordered discrete values. We prove that the TV-
are the sets of linearly-ordered discrete values. We prove that the TV-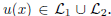 This extends the results for the global optimization of the discrete-constrained TV-
This extends the results for the global optimization of the discrete-constrained TV-