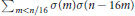Refine search
Actions for selected content:
3 results
Generalized divisor functions in arithmetic progressions: II
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 16 November 2023, pp. 28-56
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Averages of shifted convolutions of d3(n)
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 3 / October 2012
- Published online by Cambridge University Press:
- 12 April 2012, pp. 551-576
-
- Article
-
- You have access
- Export citation
The Convolution Sum Σm<n/16σ(m)σ(n – 16m)
-
- Journal:
- Canadian Mathematical Bulletin / Volume 51 / Issue 1 / 01 March 2008
- Published online by Cambridge University Press:
- 20 November 2018, pp. 3-14
- Print publication:
- 01 March 2008
-
- Article
-
- You have access
- Export citation