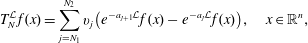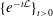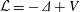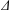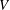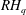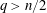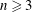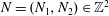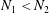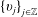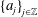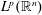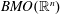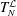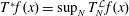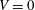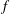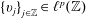Refine search
Actions for selected content:
1 results
Boundedness of Differential Transforms for Heat Semigroups Generated by Schrödinger Operators
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 12 February 2020, pp. 622-655
- Print publication:
- June 2021
-
- Article
- Export citation
-
In this paper we analyze the convergence of the following type of series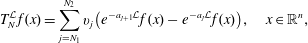
where
$$\begin{eqnarray}T_{N}^{{\mathcal{L}}}f(x)=\mathop{\sum }_{j=N_{1}}^{N_{2}}v_{j}\big(e^{-a_{j+1}{\mathcal{L}}}f(x)-e^{-a_{j}{\mathcal{L}}}f(x)\big),\quad x\in \mathbb{R}^{n},\end{eqnarray}$$
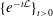${\{e^{-t{\mathcal{L}}}\}}_{t>0}$ is the heat semigroup of the operator 
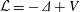${\mathcal{L}}=-\unicode[STIX]{x1D6E5}+V$ with 
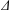$\unicode[STIX]{x1D6E5}$ being the classical laplacian, the nonnegative potential 
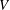$V$ belonging to the reverse Hölder class 
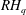$RH_{q}$ with 
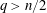$q>n/2$ and 
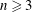$n\geqslant 3$, 
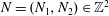$N=(N_{1},N_{2})\in \mathbb{Z}^{2}$ with 
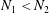$N_{1}<N_{2}$, 
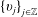${\{v_{j}\}}_{j\in \mathbb{Z}}$ is a bounded real sequences, and 
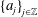${\{a_{j}\}}_{j\in \mathbb{Z}}$ is an increasing real sequence.Our analysis will consist in the boundedness, in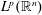
$L^{p}(\mathbb{R}^{n})$ and in 
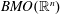$BMO(\mathbb{R}^{n})$, of the operators 
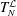$T_{N}^{{\mathcal{L}}}$ and its maximal operator 
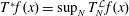$T^{\ast }f(x)=\sup _{N}T_{N}^{{\mathcal{L}}}f(x)$.It is also shown that the local size of the maximal differential transform operators (with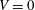
$V=0$) is the same with the order of a singular integral for functions 
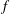$f$ having local support. Moreover, if 
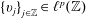${\{v_{j}\}}_{j\in \mathbb{Z}}\in \ell ^{p}(\mathbb{Z})$, we get an intermediate size between the local size of singular integrals and Hardy–Littlewood maximal operator.
