We prove that any continuous function can be locally approximated at a fixed point 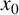 $x_{0}$ by an uncountable family resistant to disruptions by the family of continuous functions for which
$x_{0}$ by an uncountable family resistant to disruptions by the family of continuous functions for which  $x_{0}$ is a fixed point. In that context, we also consider the property of quasicontinuity.
$x_{0}$ is a fixed point. In that context, we also consider the property of quasicontinuity.