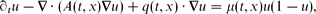Refine search
Actions for selected content:
3 results
Some new functionals related to free boundary minimal submanifolds
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 02 February 2026, pp. 1-26
-
- Article
- Export citation
Global minimizer of the ground state for two phase conductorsin low contrast regime∗∗∗
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 20 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 03 March 2014, pp. 362-388
- Print publication:
- April 2014
-
- Article
- Export citation
Some dependence results between the spreading speed and the coefficients of the space–time periodic Fisher–KPP equation
-
- Journal:
- European Journal of Applied Mathematics / Volume 22 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 28 February 2011, pp. 169-185
-
- Article
- Export citation