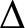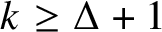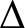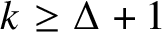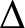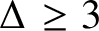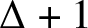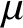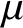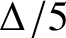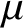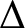Hajnal and Szemerédi proved that if G is a finite graph with maximum degree 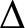$\Delta $, then for every integer 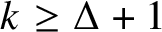$k \geq \Delta +1$, G has a proper colouring with k colours in which every two colour classes differ in size at most by 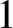$1$; such colourings are called equitable. We obtain an analogue of this result for infinite graphs in the Borel setting. Specifically, we show that if G is an aperiodic Borel graph of finite maximum degree 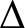$\Delta $, then for each 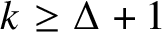$k \geq \Delta + 1$, G has a Borel proper k-colouring in which every two colour classes are related by an element of the Borel full semigroup of G. In particular, such colourings are equitable with respect to every G-invariant probability measure. We also establish a measurable version of a result of Kostochka and Nakprasit on equitable $\Delta $-colourings of graphs with small average degree. Namely, we prove that if 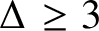$\Delta \geq 3$, G does not contain a clique on 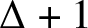$\Delta + 1$ vertices and 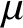$\mu $ is an atomless G-invariant probability measure such that the average degree of G with respect to 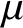$\mu $ is at most 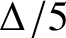$\Delta /5$, then G has a 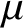$\mu $-equitable 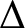$\Delta $-colouring. As steps toward the proof of this result, we establish measurable and list-colouring extensions of a strengthening of Brooks’ theorem due to Kostochka and Nakprasit.