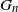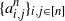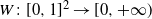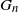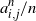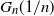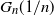Refine search
Actions for selected content:
1 results
The k-core in percolated dense graph sequences
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 08 October 2024, pp. 298-318
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
We determine the order of the k-core in a large class of dense graph sequences. Let
$G_n$ be a sequence of undirected, n-vertex graphs with edge weights 
$\{a^n_{i,j}\}_{i,j \in [n]}$ that converges to a graphon 
$W\colon[0,1]^2 \to [0,+\infty)$ in the cut metric. Keeping an edge (i,j) of 
$G_n$ with probability 
${a^n_{i,j}}/{n}$ independently, we obtain a sequence of random graphs 
$G_n({1}/{n})$. Using a branching process and the theory of dense graph limits, under mild assumptions we obtain the order of the k-core of random graphs 
$G_n({1}/{n})$. Our result can also be used to obtain the threshold of appearance of a k-core of order n.
