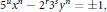Skip to main content Accessibility help
×
  1. Home
  2. Search

Refine search

Refine search

Access:
Content type:
Publication date:
Apply   From and To filters
Subject: Show more
Journals Show more
Publishers: Show more
Societies Show more
Series: Show more
Collections: Show more

Actions for selected content:

Select all | Deselect all
  • View selected items
  • Export citations
  • Download PDF (zip)
  • Save to Kindle
  • Save to Dropbox
  • Save to Google Drive

Save Search

You can save your searches here and later view and run them again in "My saved searches".

Please provide a title, maximum of 40 characters.
Cancel
×

2 results

  • A Multi-Frey Approach to Some Multi-Parameter Families of Diophantine Equations

  • Yann Bugeaud, Maurice Mignotte, Samir Siksek
  • Journal:
    Canadian Journal of Mathematics / Volume 60 / Issue 3 / 01 June 2008
    Published online by Cambridge University Press:
    20 November 2018, pp. 491-519
    Print publication:
    01 June 2008
    • Article
      • You have access
    • PDF
    • Export citation

  • We solve several multi-parameter families of binomial Thue equations of arbitrary degree; for example, we solve the equation

    $${{5}^{u}}{{x}^{n}}-{{2}^{r}}{{3}^{5}}{{y}^{n}}=\pm 1,$$

    in non-zero integers $x,y$ and positive integers $u,r,s$ and $n\ge 3$ . Our approach uses several Frey curves simultaneously, Galois representations and level-lowering, new lower bounds for linear forms in 3 logarithms due to Mignotte and a famous theorem of Bennett on binomial Thue equations.

  • Classical and modular approaches to exponential Diophantine equations II. The Lebesgue–Nagell equation

  • Yann Bugeaud, Maurice Mignotte, Samir Siksek
  • Journal:
    Compositio Mathematica / Volume 142 / Issue 1 / January 2006
    Published online by Cambridge University Press:
    13 January 2006, pp. 31-62
    Print publication:
    January 2006
    • Article
      • You have access
    • PDF
    • Export citation

  • This is the second in a series of papers where we combine the classical approach to exponential Diophantine equations (linear forms in logarithms, Thue equations, etc.) with a modular approach based on some of the ideas of the proof of Fermat's Last Theorem. In this paper we use a general and powerful new lower bound for linear forms in three logarithms, together with a combination of classical, elementary and substantially improved modular methods to solve completely the Lebesgue–Nagell equation x2 + D = yn, x, y integers, $n\geq 3$, for D in the range $1 \leq D \leq 100$.