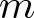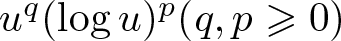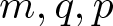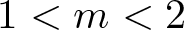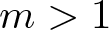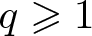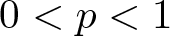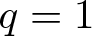This paper is concerned with Liouville-type theorems of positive weak solutions to elliptic 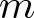$m$-Laplace equation and inequality with the logarithmic nonlinearity 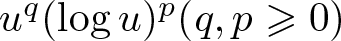$u^q(\log u)^p (q,p\geqslant0)$. Using a direct Bernstein method we obtain a first range of values of 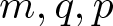$m,q,p$ in which all positive weak solutions of equation are constants, this holds in the following cases: (i) 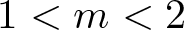$1 \lt m \lt 2$, $m-1 \lt q \lt 1$, $0 \lt p \lt q$; (ii) 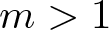$m \gt 1$, 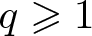$q\geqslant1$, 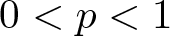$0 \lt p \lt 1$. When 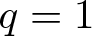$q=1$, the positive weak solutions are required to be bounded. Based on transformation of inequality and the utilization of suitable cut-off functions, we establish a Liouville-type theorem for positive weak solutions of inequality; this result also remains valid on complete noncompact Riemannian manifold.

In this paper, we study the Cauchy problem for pseudo-parabolic equations with a logarithmic nonlinearity. After establishing the existence and uniqueness of weak solutions within a suitable functional framework, we investigate several qualitative properties, including the asymptotic behaviour and blow-up of solutions as $t\to +\infty$. Moreover, when the initial data are close to a Gaussian function, we prove that these weak solutions exhibit either super-exponential growth or super-exponential decay.