Henle, Mathias, and Woodin proved in [21] that, provided that 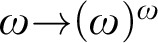${\omega }{\rightarrow }({\omega })^{{\omega }}$ holds in a model M of ZF, then forcing with 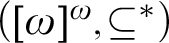$([{\omega }]^{{\omega }},{\subseteq }^*)$ over M adds no new sets of ordinals, thus earning the name a “barren” extension. Moreover, under an additional assumption, they proved that this generic extension preserves all strong partition cardinals. This forcing thus produces a model 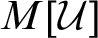$M[\mathcal {U}]$, where 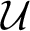$\mathcal {U}$ is a Ramsey ultrafilter, with many properties of the original model M. This begged the question of how important the Ramseyness of 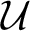$\mathcal {U}$ is for these results. In this paper, we show that several classes of 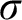$\sigma $-closed forcings which generate non-Ramsey ultrafilters have the same properties. Such ultrafilters include Milliken–Taylor ultrafilters, a class of rapid p-points of Laflamme, k-arrow p-points of Baumgartner and Taylor, and extensions to a class of ultrafilters constructed by Dobrinen, Mijares, and Trujillo. Furthermore, the class of Boolean algebras 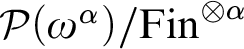$\mathcal {P}({\omega }^{{\alpha }})/{\mathrm {Fin}}^{\otimes {\alpha }}$, 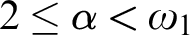$2\le {\alpha }<{\omega }_1$, forcing non-p-points also produce barren extensions.