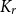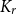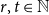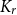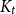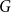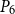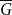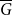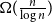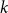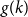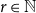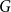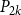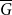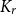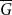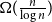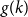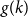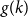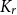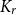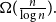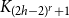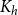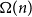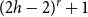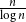A well-known theorem of Nikiforov asserts that any graph with a positive 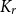$K_{r}$-density contains a logarithmic blowup of 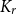$K_r$. In this paper, we explore variants of Nikiforov’s result in the following form. Given 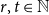$r,t\in \mathbb{N}$, when a positive 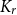$K_{r}$-density implies the existence of a significantly larger (with almost linear size) blowup of 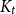$K_t$? Our results include:

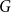• • For an $n$-vertex ordered graph $G$ with no induced monotone path 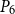$P_{6}$, if its complement 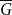$\overline {G}$ has positive triangle density, then 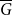$\overline {G}$ contains a biclique of size 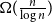$\Omega ({n \over {\log n}})$. This strengthens a recent result of Pach and Tomon. For general 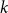$k$, let 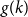$g(k)$ be the minimum 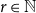$r\in \mathbb{N}$ such that for any $n$-vertex ordered graph 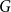$G$ with no induced monotone 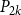$P_{2k}$, if 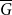$\overline {G}$ has positive 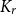$K_r$-density, then 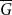$\overline {G}$ contains a biclique of size 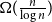$\Omega ({n \over {\log n}})$. Using concentration of measure and the isodiametric inequality on high dimensional spheres, we provide constructions showing that, surprisingly, 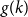$g(k)$ grows quadratically. On the other hand, we relate the problem of upper bounding 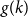$g(k)$ to a certain Ramsey problem and determine 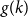$g(k)$ up to a factor of 2.

• • Any incomparability graph with positive 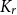$K_{r}$-density contains a blowup of 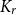$K_r$ of size 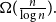$\Omega ({n \over {\log n}}).$ This confirms a conjecture of Tomon in a stronger form. In doing so, we obtain a strong regularity type lemma for incomparability graphs with no large blowups of a clique, which is of independent interest. We also prove that any $r$-comparability graph with positive 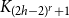$K_{(2h-2)^{r}+1}$-density contains a blowup of 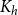$K_h$ of size 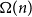$\Omega (n)$, where the constant 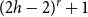$(2h-2)^{r}+1$ is optimal.

The 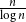${n \over {\log n}}$ size of the blowups in all our results are optimal up to a constant factor.