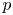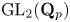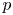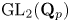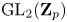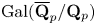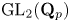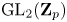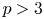Refine search
Actions for selected content:
1 results
Restriction of p-adic representations of GL2(Qp) to parahoric subgroups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 24 March 2025, pp. 74-119
- Print publication:
- January 2025
-
- Article
- Export citation
-
Without using the
$p$-adic Langlands correspondence, we prove that for many finite-length smooth representations of 
$\mathrm {GL}_2(\mathbf {Q}_p)$ on 
$p$-torsion modules the 
$\mathrm {GL}_2(\mathbf {Q}_p)$-linear morphisms coincide with the morphisms that are linear for the normalizer of a parahoric subgroup. We identify this subgroup to be the Iwahori subgroup in the supersingular case, and 
$\mathrm {GL}_2(\mathbf {Z}_p)$ in the principal series case. As an application, we relate the action of parahoric subgroups to the action of the inertia group of 
$\mathrm {Gal}(\overline {\mathbf {Q}}_p/\mathbf {Q}_p)$, and we prove that if an irreducible Banach space representation 
$\Pi$ of 
$\mathrm {GL}_2(\mathbf {Q}_p)$ has infinite 
$\mathrm {GL}_2(\mathbf {Z}_p)$-length, then a twist of 
$\Pi$ has locally algebraic vectors. This answers a question of Dospinescu. We make the simplifying assumption that 
$p > 3$ and that all our representations are generic.
