This thesis is concerned with the expansions of algebraic structures and their fit in Shelah’s classification landscape.
The first part deals with the expansion of a theory by a random predicate for a substructure model of a reduct of the theory. Let T be a theory in a language 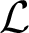 $\mathcal {L}$. Let
$\mathcal {L}$. Let 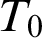 $T_0$ be a reduct of T. Let
$T_0$ be a reduct of T. Let 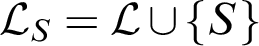 $\mathcal {L}_S = \mathcal {L}\cup \{S\}$, for S a new unary predicate symbol, and
$\mathcal {L}_S = \mathcal {L}\cup \{S\}$, for S a new unary predicate symbol, and 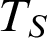 $T_S$ be the
$T_S$ be the 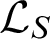 $\mathcal {L}_S$-theory that axiomatises the following structures:
$\mathcal {L}_S$-theory that axiomatises the following structures: 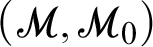 $(\mathscr {M},\mathscr {M}_0)$ consist of a model
$(\mathscr {M},\mathscr {M}_0)$ consist of a model 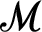 $\mathscr {M}$ of T and S is a predicate for a model
$\mathscr {M}$ of T and S is a predicate for a model  $\mathscr {M}_0$ of
$\mathscr {M}_0$ of 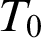 $T_0$ which is a substructure of
$T_0$ which is a substructure of 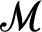 $\mathscr {M}$. We present a setting for the existence of a model-companion
$\mathscr {M}$. We present a setting for the existence of a model-companion 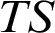 $TS$ of
$TS$ of 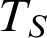 $T_S$. As a consequence, we obtain the existence of the model-companion of the following theories, for
$T_S$. As a consequence, we obtain the existence of the model-companion of the following theories, for 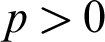 $p>0$ a prime number:
$p>0$ a prime number:
From an independence relation
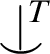
in
T, we define independence relations in
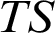 $TS$
$TS$ and identify which properties of
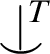
are transferred to those new independence relations in
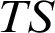 $TS$
$TS$, and under which conditions. This allows us to exhibit hypotheses under which the expansion from
T to
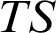 $TS$
$TS$ preserves
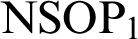 $\mathrm {NSOP}_{1}$
$\mathrm {NSOP}_{1}$, simplicity, or stability. In particular, under some technical hypothesis on
T, we may draw the following picture (the left column implies the right column):
Configuration 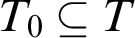 $T_0\subseteq T$ $T_0\subseteq T$ | Generic expansion 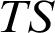 $TS$ $TS$ |
|---|
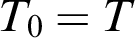 $T_0 = T$ $T_0 = T$ | Preserves stability |
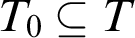 $T_0\subseteq T$ $T_0\subseteq T$ | Preserves 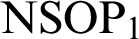 $\mathrm {NSOP}_{1}$ $\mathrm {NSOP}_{1}$ |
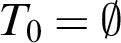 $T_0 = \emptyset $ $T_0 = \emptyset $ | Preserves simplicity |
In particular, this construction produces new examples of 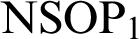 $\mathrm {NSOP}_{1}$ not simple theories, and we study in depth a particular example: the expansion of an algebraically closed field of positive characteristic by a generic additive subgroup. We give a full description of imaginaries, forking, and Kim-forking in this example.
$\mathrm {NSOP}_{1}$ not simple theories, and we study in depth a particular example: the expansion of an algebraically closed field of positive characteristic by a generic additive subgroup. We give a full description of imaginaries, forking, and Kim-forking in this example.
The second part studies expansions of the group of integers by p-adic valuations. We prove quantifier elimination in a natural language and compute the dp-rank of these expansions: it equals the number of independent p-adic valuations considered. Thus, the expansion of the integers by one p-adic valuation is a new dp-minimal expansion of the group of integers. Finally, we prove that the latter expansion does not admit intermediate structures: any definable set in the expansion is either definable in the group structure or is able to “reconstruct” the valuation using only the group operation.
Abstract prepared by Christian d’Elbée.
E-mail: delbee@math.univ-lyon1.fr
URL: https://choum.net/~chris/page_perso