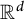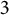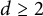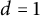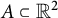Refine search
Actions for selected content:
2 results
Triangles in the plane and arithmetic progressions in thick compact subsets of
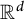 $\mathbb {R}^d$
$\mathbb {R}^d$
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 23 January 2026, pp. 1-41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stein’s method and approximating the multidimensional quantum harmonic oscillator
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 11 April 2023, pp. 855-873
- Print publication:
- September 2023
-
- Article
-
- You have access
- HTML
- Export citation