We study the existence of reducing subspaces for rank-one perturbations of diagonal operators and, in general, of normal operators of uniform multiplicity one. As we will show, the spectral picture will play a significant role in order to prove the existence of reducing subspaces for rank-one perturbations of diagonal operators whenever they are not normal. In this regard, the most extreme case is provided when the spectrum of the rank-one perturbation of a diagonal operator $T=D + u\otimes v$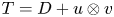 (uniquely determined by such expression) is contained in a line, since in such a case $T$
(uniquely determined by such expression) is contained in a line, since in such a case $T$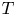 has a reducing subspace if and only if $T$
has a reducing subspace if and only if $T$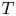 is normal. Nevertheless, we will show that it is possible to exhibit non-normal operators $T=D + u\otimes v$
is normal. Nevertheless, we will show that it is possible to exhibit non-normal operators $T=D + u\otimes v$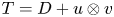 with spectrum contained in a circle either having or lacking non-trivial reducing subspaces. Moreover, as far as the spectrum of $T$
with spectrum contained in a circle either having or lacking non-trivial reducing subspaces. Moreover, as far as the spectrum of $T$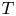 is contained in any compact subset of the complex plane, we provide a characterization of the reducing subspaces $M$
is contained in any compact subset of the complex plane, we provide a characterization of the reducing subspaces $M$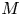 of $T$
of $T$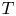 such that the restriction $T\mid _M$
such that the restriction $T\mid _M$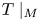 is normal. In particular, such characterization allows us to exhibit rank-one perturbations of completely normal diagonal operators (in the sense of Wermer) lacking reducing subspaces. Furthermore, it determines completely the decomposition of the underlying Hilbert space in an orthogonal sum of reducing subspaces in the context of a classical theorem due to Behncke on essentially normal operators.
is normal. In particular, such characterization allows us to exhibit rank-one perturbations of completely normal diagonal operators (in the sense of Wermer) lacking reducing subspaces. Furthermore, it determines completely the decomposition of the underlying Hilbert space in an orthogonal sum of reducing subspaces in the context of a classical theorem due to Behncke on essentially normal operators.