In this paper, we are interested in the existence and concentration of normalized solutions for the following logarithmic Schrödinger–Bopp–Podolsky type system involving the 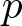$p$-Laplacian in 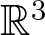$\mathbb{R}^3$:

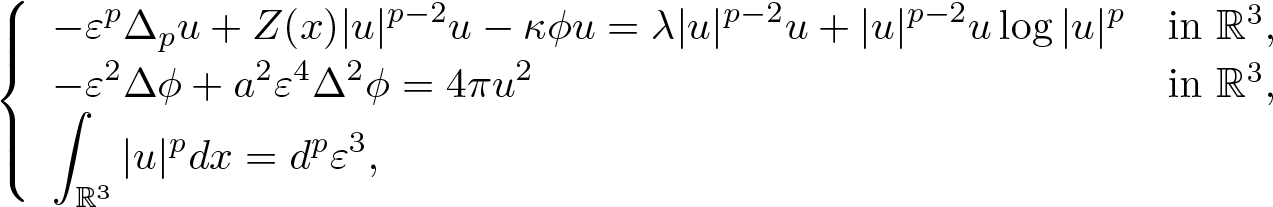\begin{equation*}\left\{\begin{array}{ll}\displaystyle -\varepsilon^p\Delta_p u+Z(x)|u|^{p-2}u-\kappa\phi u=\lambda |u|^{p-2}u+|u|^{p-2}u\log|u|^p& \text{in} \ \mathbb{R}^3, \\\displaystyle -\varepsilon^2\Delta\phi+a^2\varepsilon^4\Delta^2\phi=4\pi u^2& \text{in} \ \mathbb{R}^3, \\\displaystyle \int_{\mathbb{R}^3}|u|^pdx=d^p\varepsilon^3,\end{array}\right.\end{equation*}

where 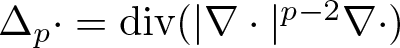$\Delta_p\cdot =\text{div} (|\nabla \cdot|^{p-2}\nabla \cdot)$ denotes the usual 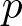$p$-Laplacian operator, 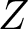$Z$ is a given external potential, 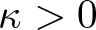$\kappa \gt 0$ a constant, 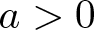$a \gt 0$ is the Bopp–Podolsky constant and 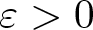$\varepsilon \gt 0$ is a small parameter. The unknowns are 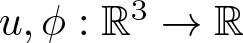$u,\phi:\mathbb{R}^{3}\to \mathbb{R}$ and the Lagrange multiplier 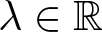$\lambda\in\mathbb{R}$. If 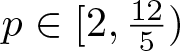$p\in[2,\frac{12}{5})$, we obtain, via the variational method, that the number of positive solutions depends on the profile of 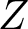$Z$ and the solutions concentrate around the global minimum points of 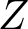$Z$ in the semiclassical limit as 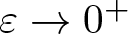$\varepsilon\to 0^{+}$.

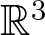
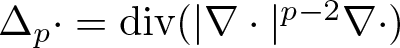
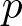
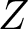
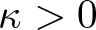
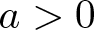
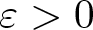
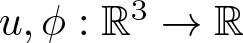
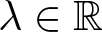
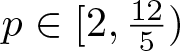
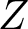
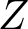
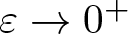
In this paper, we study the numerical solution of singularly perturbed time-dependent convection-diffusion problems. To solve these problems, the backward Euler method is first applied to discretize the time derivative on a uniform mesh, and the classical upwind finite difference scheme is used to approximate the spatial derivative on an arbitrary nonuniform grid. Then, in order to obtain an adaptive grid for all temporal levels, we construct a positive monitor function, which is similar to the arc-length monitor function. Furthermore, the ε-uniform convergence of the fully discrete scheme is derived for the numerical solution. Finally, some numerical results are given to support our theoretical results.

In this paper, we consider a singularly perturbed convection-diffusion problem. The problem involves two small parameters that gives rise to two boundary layers at two endpoints of the domain. For this problem, a non-monotone finite element methods is used. A priori error bound in the maximum norm is obtained. Based on the a priori error bound, we show that there exists Bakhvalov-type mesh that gives optimal error bound of (N−2) which is robust with respect to the two perturbation parameters. Numerical results are given that confirm the theoretical result.