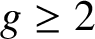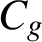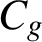Étant donnée une suite  $A = (a_n)_{n\geqslant 0}$ d’entiers naturels tous au moins égaux à 2, on pose
$A = (a_n)_{n\geqslant 0}$ d’entiers naturels tous au moins égaux à 2, on pose  $q_0 = 1$ et, pour tout entier naturel n,
$q_0 = 1$ et, pour tout entier naturel n,  $q_{n+1} = a_n q_n$. Tout nombre entier naturel
$q_{n+1} = a_n q_n$. Tout nombre entier naturel  $n\geqslant 1$ admet une unique représentation dans la base A, dite de Cantor, de la forme
$n\geqslant 1$ admet une unique représentation dans la base A, dite de Cantor, de la forme  $$ \begin{align*} m = \sum_{j\geqslant 0}\varepsilon_j(m)q_j\quad \text{avec} \quad 0\leqslant \varepsilon_j(m) < a_j = \frac{q_{j+1}}{q_j}. \end{align*} $$
$$ \begin{align*} m = \sum_{j\geqslant 0}\varepsilon_j(m)q_j\quad \text{avec} \quad 0\leqslant \varepsilon_j(m) < a_j = \frac{q_{j+1}}{q_j}. \end{align*} $$ $$ \begin{align*} S = \sum_{n \leqslant x}\Lambda(n) f(n) \end{align*} $$
$$ \begin{align*} S = \sum_{n \leqslant x}\Lambda(n) f(n) \end{align*} $$ $\Lambda $ est la fonction de von Mangoldt et f une fonction fortement multiplicative en base A. L’estimation des sommes de type I et II associées repose sur le bon contrôle de transformées de Fourier discrètes de fonctions construites à partir de f par décalage dans la numération en base A. Cette approche pouvant échouer si la suite
$\Lambda $ est la fonction de von Mangoldt et f une fonction fortement multiplicative en base A. L’estimation des sommes de type I et II associées repose sur le bon contrôle de transformées de Fourier discrètes de fonctions construites à partir de f par décalage dans la numération en base A. Cette approche pouvant échouer si la suite  $(a_n)_{n\geqslant 0}$ est trop irrégulière, nous introduisons la notion de base de Cantor tempérée et obtenons dans ce cadre une majoration générale de la somme S.
$(a_n)_{n\geqslant 0}$ est trop irrégulière, nous introduisons la notion de base de Cantor tempérée et obtenons dans ce cadre une majoration générale de la somme S.
Nous étudions plusieurs exemples dans la base  $A = (j+2)_{j\geqslant 0}$, dite factorielle. En particulier, si
$A = (j+2)_{j\geqslant 0}$, dite factorielle. En particulier, si  $s_A$ désigne la fonction somme de chiffres dans cette base et p parcourt la suite des nombres premiers, nous montrons que la suite
$s_A$ désigne la fonction somme de chiffres dans cette base et p parcourt la suite des nombres premiers, nous montrons que la suite  $(s_A(p))_{p\in \mathcal {P}}$ est bien répartie dans les progressions arithmétiques, et que la suite
$(s_A(p))_{p\in \mathcal {P}}$ est bien répartie dans les progressions arithmétiques, et que la suite  $(\alpha s_A(p))_{p\in \mathcal {P}}$ est équirépartie modulo
$(\alpha s_A(p))_{p\in \mathcal {P}}$ est équirépartie modulo  $1$ pour tout nombre irrationnel
$1$ pour tout nombre irrationnel  $\alpha $.
$\alpha $.