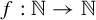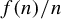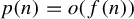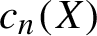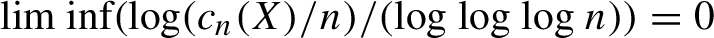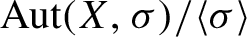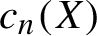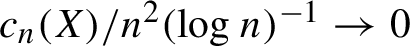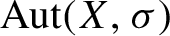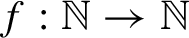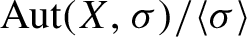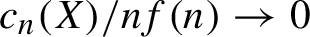We exhibit, for arbitrary $\epsilon> 0$, subshifts admitting weakly mixing (probability) measures with word complexity p satisfying $\limsup p(q) / q < 1.5 + \epsilon $. For arbitrary $f(q) \to \infty $, said subshifts can be made to satisfy $p(q) < q + f(q)$ infinitely often. We establish that every subshift associated to a rank-one transformation (on a probability space) which is not an odometer satisfies $\limsup p(q) - 1.5q = \infty $ and that this is optimal for rank-ones.

We introduce a class of rank-one transformations, which we call extremely elevated staircase transformations. We prove that they are measure-theoretically mixing and, for any $f : \mathbb {N} \to \mathbb {N}$ with $f(n)/n$ increasing and $\sum 1/f(n) < \infty $, that there exists an extremely elevated staircase with word complexity $p(n) = o(f(n))$. This improves the previously lowest known complexity for mixing subshifts, resolving a conjecture of Ferenczi.

We prove that for any transitive subshift X with word complexity function 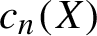$c_n(X)$, if 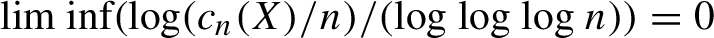$\liminf ({\log (c_n(X)/n)}/({\log \log \log n})) = 0$, then the quotient group 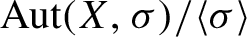${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$ of the automorphism group of X by the subgroup generated by the shift $\sigma $ is locally finite. We prove that significantly weaker upper bounds on 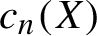$c_n(X)$ imply the same conclusion if the gap conjecture from geometric group theory is true. Our proofs rely on a general upper bound for the number of automorphisms of X of range n in terms of word complexity, which may be of independent interest. As an application, we are also able to prove that for any subshift X, if 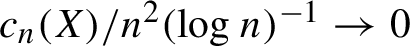${c_n(X)}/{n^2 (\log n)^{-1}} \rightarrow 0$, then 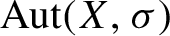$\mathrm {Aut}(X,\sigma )$ is amenable, improving a result of Cyr and Kra. In the opposite direction, we show that for any countable infinite locally finite group G and any unbounded increasing 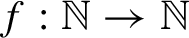$f: \mathbb {N} \rightarrow \mathbb {N}$, there exists a minimal subshift X with 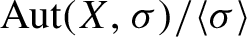${{\mathrm {Aut}(X,\sigma )}/{\langle \sigma \rangle }}$ isomorphic to G and 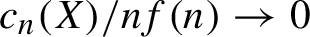${c_n(X)}/{nf(n)} \rightarrow 0$.