Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-10T19:49:13.940Z Has data issue: false hasContentIssue false
  • English
  • Français

Heat or mass transport from drops in shearing flows. Part 1. The open-streamline regime

Published online by Cambridge University Press:  06 July 2018

Deepak Krishnamurthy  and
Ganesh Subramanian Open the ORCID record for Ganesh Subramanian [Opens in a new window]
Deepak Krishnamurthy
Affiliation:
Bioengineering Department, Stanford University, Shriram Center, Room 064, 443 Via Ortega, Stanford, CA 94305-4125, USA
Ganesh Subramanian*
Affiliation:
Engineering Mechanics Unit, Jawaharlal Nehru Centre for Advanced Scientific Research, Bangalore, Karnataka 560064, India
*
†Email address for correspondence: sganesh@jncasr.ac.in
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the heat or mass transfer from a neutrally buoyant spherical drop embedded in an ambient Newtonian medium, undergoing a general shearing flow, in the strong convection limit. The latter limit corresponds to the drop Péclet number being large (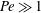$Pe\gg 1$). We consider two families of ambient linear flows: (i) planar linear flows with open streamlines (parametrized by $\unicode[STIX]{x1D6FC}$ with 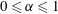$0\leqslant \unicode[STIX]{x1D6FC}\leqslant 1$, the extremal members being simple shear flow (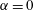$\unicode[STIX]{x1D6FC}=0$) and planar extension (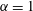$\unicode[STIX]{x1D6FC}=1$)) and (ii) three-dimensional extensional flows (parameterized by $\unicode[STIX]{x1D716}$, with 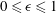$0\leqslant \unicode[STIX]{x1D716}\leqslant 1$, the extremal members being planar (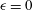$\unicode[STIX]{x1D716}=0$) and axisymmetric extension (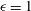$\unicode[STIX]{x1D716}=1$)). For the first family, an analysis of the exterior flow field in the inertialess limit (the drop Reynolds number, 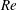$Re$, being vanishingly small) shows that there exist two distinct streamline topologies separated by a critical drop-to-medium viscosity ratio (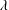$\unicode[STIX]{x1D706}$) given by 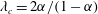$\unicode[STIX]{x1D706}_{c}=2\unicode[STIX]{x1D6FC}/(1-\unicode[STIX]{x1D6FC})$. For 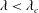$\unicode[STIX]{x1D706}<\unicode[STIX]{x1D706}_{c}$ all streamlines are open, while the near-field streamlines are closed for 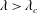$\unicode[STIX]{x1D706}>\unicode[STIX]{x1D706}_{c}$. For the second family, the exterior streamlines remain open regardless of 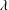$\unicode[STIX]{x1D706}$. The two streamline topologies lead to qualitatively different mechanisms of transport for large 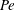$Pe$. The transport in the open streamline regime is enhanced in the usual manner via the formation of a boundary layer. In sharp contrast, the closed-streamline regime displays diffusion-limited transport, so there is only a finite enhancement even as 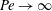$Pe\rightarrow \infty$. For 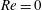$Re=0$, the drop surface streamlines in a planar linear flow may be regarded as generalized Jeffery orbits with a flow and viscosity dependent aspect ratio Jeffery orbits denote the aspect-ratio-dependent inertialess trajectories of a rigid axisymmetric particle in a simple shear flow; see Jeffery (Proc. R. Soc. Lond. A, vol. 102 (715), 1922, pp. 161–179). A Jeffery-orbit-based non-orthogonal coordinate system thus serves as a natural candidate to tackle the transport problem from a drop, in a planar linear flow, in the limit 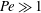$Pe\gg 1$. Use of this system allows one to derive a closed-form expression for the dimensionless rate of transport (the Nusselt number 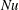$Nu$) from a drop in the open-streamline regime (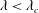$\unicode[STIX]{x1D706}<\unicode[STIX]{x1D706}_{c}$). Symmetry arguments point to a Jeffery-orbit-based coordinate system for any linear flow, and a variant of this coordinate system is therefore used to derive the Nusselt number for the family of three-dimensional extensional flows. For both classes of flows considered, the boundary-layer-enhanced transport implies that the Nusselt number takes the form 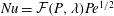$Nu={\mathcal{F}}(P,\unicode[STIX]{x1D706})Pe^{1/2}$, with the parameter 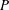$P$ being $\unicode[STIX]{x1D6FC}$ or $\unicode[STIX]{x1D716}$, and 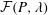${\mathcal{F}}(P,\unicode[STIX]{x1D706})$ given as a one and two-dimensional integral, respectively, which is readily evaluated numerically.

JFM classification

Drops and Bubbles: Drops and Bubbles Low-Reynolds-number flows: Low-Reynolds-number flows Multiphase and Particle-laden Flows: Multiphase and Particle-laden Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 850 , 10 September 2018 , pp. 439 - 483
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Acrivos, A. 1971 Heat transfer at high Peclet number from a small sphere freely rotating in a simple shear field. J. Fluid Mech. 46 (02), 233–240.Google Scholar
Acrivos, A. & Goddard, J. D. 1965 Asymptotic expansions for laminar forced-convection heat and mass transfer. J. Fluid Mech. 23 (02), 273–291.Google Scholar
Aris, R. 2012 Vectors, Tensors and the Basic Equations of Fluid Mechanics. Dover.Google Scholar
Batchelor, G. K. 1979 Mass transfer from a particle suspended in fluid with a steady linear ambient velocity distribution. J. Fluid Mech. 95 (02), 369–400.Google Scholar
Batchelor, G. K. 1980 Mass transfer from small particles suspended in turbulent fluid. J. Fluid Mech. 98 (3), 609–623.Google Scholar
Batchelor, G. K. 2000 An Introduction to Fluid Dynamics. Cambridge University Press.Google Scholar
Beard, K. V. & Pruppacher, H. R. 1971 A wind tunnel investigation of the rate of evaporation of small water drops falling at terminal velocity in air. J. Atmos. Sci. 28 (8), 1455–1464.Google Scholar
Brenner, H. 1967 On the invariance of the heat-transfer coefficient to flow reversal in Stokes and potential streaming flows past particles of arbitrary shape (forced convection heat transfer coefficient invariance to flow reversal in Stokes and potential streaming flows past isothermal particles of arbitrary shape). J. Math. Phys. Sci. 1, 173–179.Google Scholar
Brenner, H. 1970 Invariance of the overall mass transfer coefficient to flow reversal during Stokes flow past one or more particles of arbitrary shape. In Chem. Engng Process Symp. Series, pp. 123–126.Google Scholar
Brooks, B. 2010 Suspension polymerization processes. Chem. Engng Technol. 33 (11), 1737–1744.Google Scholar
Bryden, M. D. & Brenner, H. 1999 Mass-transfer enhancement via chaotic laminar flow within a droplet. J. Fluid Mech. 379, 319–331.Google Scholar
Edelmann, C. A., Le Clercq, P. C. & Noll, B. 2017 Numerical investigation of different modes of internal circulation in spherical drops: fluid dynamics and mass/heat transfer. Intl J. Multiphase Flow 95, 54–70.Google Scholar
Chao, B. T. 1969 Transient heat and mass transfer to a translating droplet. J. Heat Transfer 91, 273–281.Google Scholar
Christov, C. I. & Homsy, G. M. 2009 Enhancement of transport from drops by steady and modulated electric fields. Phys. Fluids 21, 083102.Google Scholar
Cox, R. G. 1969 The deformation of a drop in a general time-dependent fluid flow. J. Fluid Mech. 37 (03), 601–623.Google Scholar
Cox, R. G. 1971 The motion of long slender bodies in a viscous fluid. Part 2. Shear flow. J. Fluid Mech. 45 (4), 625–657.Google Scholar
Cox, R. G., Zia, I. Y. Z. & Mason, S. G. 1968 Particle motions in sheared suspensions xxv. Streamlines around cylinders and spheres. J. Colloid Interface Sci. 27 (1), 7–18.Google Scholar
Duguid, H. A. & Stampfer, J. F. Jr 1971 The evaporation rates of small, freely falling water drops. J. Atmos. Sci. 28 (7), 1233–1243.Google Scholar
Frankel, N. A. & Acrivos, A. 1968 Heat and mass transfer from small spheres and cylinders freely suspended in shear flow. Phys. Fluids 11, 1913–1918.Google Scholar
Guasto, J. S., Rusconi, R. & Stocker, R. 2012 Fluid mechanics of planktonic microorganisms. Annu. Rev. Fluid Mech. 44, 373–400.Google Scholar
Gupalo, I. P. & Riazantsev, I. S. 1972 Diffusion on a particle in the shear flow of a viscous fluid. Approximation of the diffusion boundary layer: PMM vol. 36, no 3, 1972, pp. 475–479. J. Appl. Math. Mech. 36 (3), 447–451.Google Scholar
Gupalo, I. P., Riazantsev, I. S. & Ulin, V. I. 1975 Diffusion on a particle in a homogeneous translational-shear flow. Prikl. Mat. Mekh. 39, 497–504.Google Scholar
Hinch, E. J. & Leal, L. G. 1972 The effect of Brownian motion on the rheological properties of a suspension of non-spherical particles. J. Fluid Mech. 52 (04), 683–712.Google Scholar
Ishikawa, T., Simmonds, M. P. & Pedley, T. J. 2006 Hydrodynamic interaction of two swimming model microorganisms. J. Fluid Mech. 568, 119–160.Google Scholar
Jeffery, G. B. 1922 The motion of ellipsoidal particles immersed in a viscous fluid. Proc. R. Soc. Lond. A 102 (715), 161–179.Google Scholar
Juncu, G. & Mihail, R. 1987 The effect of diffusivities ratio on conjugate mass transfer. Intl J. Heat Mass Transfer 30, 1223–1226.Google Scholar
Kao, S. V., Cox, R. G. & Mason, S. G. 1977 Streamlines around single spheres and trajectories of pairs of spheres in two-dimensional creeping flows. Chem. Engng Sci. 32 (12), 1505–1515.Google Scholar
Kennedy, M. R., Pozrikidis, C. & Skalak, R. 1994 Motion and deformation of liquid drops, and the rheology of dilute emulsions in simple shear flow. Comput. Fluids 23 (2), 251–278.Google Scholar
Kinzer, G. D. & Gunn, R. 1951 The evaporation, temperature and thermal relaxation-time of freely falling water drops. J. Meteorol. 8 (2), 71–83.Google Scholar
Kirtland, J. D., Siegel, C. R. & Stroock, A. D. 2009 Interfacial mass transport in steady three-dimensional flows in microchannels. New J. Phys. 11, 075028.Google Scholar
Kossack, C. A & Acrivos, A. 1974 Steady simple shear flow past a circular cylinder at moderate Reynolds numbers: a numerical solution. J. Fluid Mech. 66 (02), 353–376.Google Scholar
Krishnamurthy, D. & Subramanian, G. 2018 Heat or mass transport from drops in shearing flows. Part 2. Inertial effects on transport. J. Fluid Mech. 850, 484–524.Google Scholar
Kronig, R. & Brink, J. C. 1950 On the theory of extraction from falling droplets. Appl. Sci. Res. 2, 142–154.Google Scholar
Law, C. K. 1982 Recent advances in droplet vaporization and combustion. Prog. Energy Combust. Sci. 8 (3), 171–201.Google Scholar
Leal, L. G. & Hinch, E. J. 1971 The effect of weak Brownian rotations on particles in shear flow. J. Fluid Mech. 46 (04), 685–703.Google Scholar
Leal, L. G. 2007 Advanced Transport Phenomena: Fluid Mechanics and Convective Transport Processes, vol. 7. Cambridge University Press.Google Scholar
Magar, V., Goto, T. & Pedley, T. J. 2003 Nutrient uptake by a self-propelled steady squirmer. Q. J. Mech. Appl. Math. 56 (1), 65–91.Google Scholar
Magar, V. & Pedley, T. J. 2005 Average nutrient uptake by a self-propelled unsteady squirmer. J. Fluid Mech. 539, 93–112.Google Scholar
Marath, N. K. & Subramanian, G. 2018 The inertial orientation dynamics of anisotropic particles in planar linear flows. J. Fluid Mech. 844, 357–402.Google Scholar
Michaelides, E. E. 2003 Hydrodynamic force and heat/mass transfer from particles, bubbles, and drops – the Freeman Scholar Lecture. J. Fluids Engng 125 (2), 209–238.Google Scholar
Oliver, D. L. R., Carleson, T. E. & Chung, J. N. 1985 Transient heat transfer to a fluid sphere suspended in an electric field. Trans. ASME 28, 1005–1009.Google Scholar
Oliver, D. L. R. & De Witt, K. J. 1993 High Peclet number heat transfer from a droplet suspended in an electric field: interior problem. Intl J. Heat Mass Transfer 36, 3153–3155.Google Scholar
Oliver, D. L. R. & Souccar, A. W. 2006 Heat transfer from a translating droplet a high Peclet numbers: revisiting the classic solution Kronig and Brink. Trans. ASME 128, 648–652.Google Scholar
Pedley, T. J., Brumley, D. R. & Goldstein, R. E. 2016 Squirmers with swirl – a model for volvox swimming. J. Fluid Mech. 798, 165–186.Google Scholar
Poe, G. G. & Acrivos, A. 1975 Closed-streamline flows past rotating single cylinders and spheres: inertia effects. J. Fluid Mech. 72 (04), 605–623.Google Scholar
Poe, G. G. & Acrivos, A. 1976 Closed streamline flows past small rotating particles: heat transfer at high Péclet numbers. Intl J. Multiphase Flow 2 (4), 365–377.Google Scholar
Polyanin, A. D. 1984 Three-dimensional diffusive boundary-layer problems. J. Appl. Mech. Tech. Phys. 25 (4), 562–571.Google Scholar
Powell, R. L. 1983 External and internal streamlines and deformation of drops in linear two-dimensional flows. J. Colloid Interface Sci. 95 (1), 148–162.Google Scholar
Robertson, C. R. & Acrivos, A. 1970a Low Reynolds number shear flow past a rotating circular cylinder. Part 1. Momentum transfer. J. Fluid Mech. 40 (04), 685–703.Google Scholar
Robertson, C. R. & Acrivos, A. 1970b Low Reynolds number shear flow past circular cylinder. Part 2. Heat transfer. J. Fluid Mech. 40 (4), 705–718.Google Scholar
Ruckenstein, E. 1967 Mass transfer between a single drop and a continuous phase. Intl J. Heat Mass Transfer 10, 1785–1792.Google Scholar
Schlichting, H. & Gersten, K. 2001 Boundary Layer Theory. Springer.Google Scholar
Stocker, R. 2012 Marine microbes see a sea of gradients. Science 338, 628–633.Google Scholar
Stone, H. A., Nadim, A. & Strogatz, S. H. 1991 Chaotic streamlines inside drops immersed in steady Stokes flows. J. Fluid Mech. 232, 629–646.Google Scholar
Subramanian, G. & Koch, D. L. 2006a Centrifugal forces alter streamline topology and greatly enhance the rate of heat and mass transfer from neutrally buoyant particles to a shear flow. Phys. Rev. Lett. 96 (13), 134503.Google Scholar
Subramanian, G. & Koch, D. L. 2007 Heat transfer from a neutrally buoyant sphere in a second-order fluid. J. Non-Newtonian Fluid Mech. 144, 49–57.Google Scholar
Subramanian, G., Koch, D. L., Zhang, J. & Yang, C. 2011 The influence of the inertially dominated outer region on the rheology of a dilute dispersion of low-Reynolds-number drops or rigid particles. J. Fluid Mech. 674, 307–358.Google Scholar
Subramanian, G. & Koch, D. L. 2006b Inertial effects on the transfer of heat or mass from neutrally buoyant spheres in a steady linear velocity field. Phys. Fluids 18 (7), 073302.Google Scholar
Torza, S., Henry, C. P., Cox, R. G. & Mason, S. G. 1971 Particle motions in sheared suspensions. XXVI. Streamlines in and around liquid drops. J. Colloid Interface Sci. 35 (4), 529–543.Google Scholar
Trevelyan, B. J. & Mason, S. G. 1951 Particle motions in sheared suspensions. I. Rotations. J. Colloid Sci. 6 (04), 354–367.Google Scholar
Vivaldo-Lima, E., Wood, P. E., Hamielec, A. E. & Penlidis, A. 1997 An updated review on suspension polymerization. Ind. Engng Chem. Res. 36 (4), 939–965.Google Scholar
Vorotilin, V. P., Krylov, V. S. & Levich, V. G. 1965 On the theory of extraction from a falling droplet. J. Appl. Math. Mech. 29, 386–394.Google Scholar
Wegener, M., Paul, N. & Kraume, M. 2014 Fluid dynamics and mass transfer at single droplets in liquid/liquid systems. Intl J. Heat Mass Transfer 71, 475–495.Google Scholar
Yang, C., Zhang, J., Koch, D. L. & Yin, X. 2011 Mass/heat transfer from a neutrally buoyant sphere in simple shear flow at finite Reynolds and Peclet numbers. AIChE J. 57 (6), 1419–1433.Google Scholar
Yu-Fang, P. & Acrivos, A. 1968 Heat transfer at high Peclet number in regions of closed streamlines. Intl J. Heat Mass Transfer 11 (3), 439–444.Google Scholar