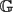Refine search
Actions for selected content:
6974 results in Algorithmics, Complexity, Computer Algebra, Computational Geometry
Acknowledgments
-
- Book:
- Analytic Pattern Matching
- Published online:
- 05 July 2015
- Print publication:
- 30 June 2015, pp xix-xx
-
- Chapter
- Export citation
Index
-
- Book:
- Analytic Pattern Matching
- Published online:
- 05 July 2015
- Print publication:
- 30 June 2015, pp 363-366
-
- Chapter
- Export citation
About the sketches
-
- Book:
- Analytic Pattern Matching
- Published online:
- 05 July 2015
- Print publication:
- 30 June 2015, pp xxi-xxii
-
- Chapter
- Export citation
Chapter 10 - String Complexity
- from II - APPLICATIONS
-
- Book:
- Analytic Pattern Matching
- Published online:
- 05 July 2015
- Print publication:
- 30 June 2015, pp 311-346
-
- Chapter
- Export citation
Chapter 3 - Constrained Exact String Matching
- from I - ANALYSIS
-
- Book:
- Analytic Pattern Matching
- Published online:
- 05 July 2015
- Print publication:
- 30 June 2015, pp 47-74
-
- Chapter
- Export citation
Chapter 2 - Exact String Matching
- from I - ANALYSIS
-
- Book:
- Analytic Pattern Matching
- Published online:
- 05 July 2015
- Print publication:
- 30 June 2015, pp 23-46
-
- Chapter
- Export citation
Chapter 1 - Probabilistic Models
- from I - ANALYSIS
-
- Book:
- Analytic Pattern Matching
- Published online:
- 05 July 2015
- Print publication:
- 30 June 2015, pp 3-22
-
- Chapter
- Export citation
II - APPLICATIONS
-
- Book:
- Analytic Pattern Matching
- Published online:
- 05 July 2015
- Print publication:
- 30 June 2015, pp 133-134
-
- Chapter
- Export citation
Chapter 5 - Subsequence String Matching
- from I - ANALYSIS
-
- Book:
- Analytic Pattern Matching
- Published online:
- 05 July 2015
- Print publication:
- 30 June 2015, pp 109-132
-
- Chapter
- Export citation
Chapter 6 - Algorithms and Data Structures
- from II - APPLICATIONS
-
- Book:
- Analytic Pattern Matching
- Published online:
- 05 July 2015
- Print publication:
- 30 June 2015, pp 135-154
-
- Chapter
- Export citation
Contents
-
- Book:
- Analytic Pattern Matching
- Published online:
- 05 July 2015
- Print publication:
- 30 June 2015, pp vii-x
-
- Chapter
- Export citation
Chapter 8 - Suffix Trees and Lempel–Ziv'77
- from II - APPLICATIONS
-
- Book:
- Analytic Pattern Matching
- Published online:
- 05 July 2015
- Print publication:
- 30 June 2015, pp 219-266
-
- Chapter
- Export citation
Foreword
-
-
- Book:
- Analytic Pattern Matching
- Published online:
- 05 July 2015
- Print publication:
- 30 June 2015, pp xi-xii
-
- Chapter
- Export citation
Preface
-
- Book:
- Analytic Pattern Matching
- Published online:
- 05 July 2015
- Print publication:
- 30 June 2015, pp xiii-xviii
-
- Chapter
- Export citation
Dedication
-
- Book:
- Analytic Pattern Matching
- Published online:
- 05 July 2015
- Print publication:
- 30 June 2015, pp v-vi
-
- Chapter
- Export citation
Chapter 4 - Generalized String Matching
- from I - ANALYSIS
-
- Book:
- Analytic Pattern Matching
- Published online:
- 05 July 2015
- Print publication:
- 30 June 2015, pp 75-108
-
- Chapter
- Export citation
Bibliography
-
- Book:
- Analytic Pattern Matching
- Published online:
- 05 July 2015
- Print publication:
- 30 June 2015, pp 347-362
-
- Chapter
- Export citation
Chapter 7 - Digital Trees
- from II - APPLICATIONS
-
- Book:
- Analytic Pattern Matching
- Published online:
- 05 July 2015
- Print publication:
- 30 June 2015, pp 155-218
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Analytic Pattern Matching
- Published online:
- 05 July 2015
- Print publication:
- 30 June 2015, pp i-iv
-
- Chapter
- Export citation
A Hitting Time Formula for the Discrete Green's Function
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 3 / May 2016
- Published online by Cambridge University Press:
- 29 June 2015, pp. 362-379
-
- Article
- Export citation