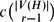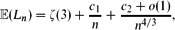Refine search
Actions for selected content:
6974 results in Algorithmics, Complexity, Computer Algebra, Computational Geometry
The Rat Game and the Mouse Game
-
-
- Book:
- Games of No Chance 4
- Published online:
- 30 May 2025
- Print publication:
- 16 April 2015, pp 95-114
-
- Chapter
- Export citation
Forcing a sparse minor
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 2 / March 2016
- Published online by Cambridge University Press:
- 16 April 2015, pp. 300-322
-
- Article
- Export citation
Contents
-
- Book:
- Games of No Chance 4
- Published online:
- 30 May 2025
- Print publication:
- 16 April 2015, pp vii-viii
-
- Chapter
- Export citation
Misère canonical forms of partizan games
-
-
- Book:
- Games of No Chance 4
- Published online:
- 30 May 2025
- Print publication:
- 16 April 2015, pp 225-240
-
- Chapter
- Export citation
Artificial intelligence for Bidding Hex
-
-
- Book:
- Games of No Chance 4
- Published online:
- 30 May 2025
- Print publication:
- 16 April 2015, pp 207-214
-
- Chapter
- Export citation
A handicap strategy for Hex
-
-
- Book:
- Games of No Chance 4
- Published online:
- 30 May 2025
- Print publication:
- 16 April 2015, pp 129-136
-
- Chapter
- Export citation
Harnessing the unwieldy MEX function
-
-
- Book:
- Games of No Chance 4
- Published online:
- 30 May 2025
- Print publication:
- 16 April 2015, pp 77-94
-
- Chapter
- Export citation
Computer analysis of Sprouts with nimbers
-
-
- Book:
- Games of No Chance 4
- Published online:
- 30 May 2025
- Print publication:
- 16 April 2015, pp 161-182
-
- Chapter
- Export citation
Orientability Thresholds for Random Hypergraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 5 / September 2015
- Published online by Cambridge University Press:
- 23 March 2015, pp. 774-824
-
- Article
- Export citation
A Combinatorial Approach to a Model of Constrained Random Walkers
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 2 / March 2016
- Published online by Cambridge University Press:
- 16 March 2015, pp. 222-235
-
- Article
- Export citation
On the Chromatic Thresholds of Hypergraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 2 / March 2016
- Published online by Cambridge University Press:
- 06 March 2015, pp. 172-212
-
- Article
- Export citation
First-Order Convergence and Roots†
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 2 / March 2016
- Published online by Cambridge University Press:
- 24 February 2015, pp. 213-221
-
- Article
- Export citation
The (7, 4)-Conjecture in Finite Groups
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 4 / July 2015
- Published online by Cambridge University Press:
- 10 February 2015, pp. 680-686
-
- Article
- Export citation

A Computational Introduction to Number Theory and Algebra
-
- Published online:
- 05 February 2015
- Print publication:
- 04 December 2008
On Directed Versions of the Hajnal–Szemerédi Theorem
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 6 / November 2015
- Published online by Cambridge University Press:
- 05 February 2015, pp. 873-928
-
- Article
- Export citation
Monotone Cellular Automata in a Random Environment
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 4 / July 2015
- Published online by Cambridge University Press:
- 02 February 2015, pp. 687-722
-
- Article
- Export citation
Easily Testable Graph Properties
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 4 / July 2015
- Published online by Cambridge University Press:
- 02 February 2015, pp. 646-657
-
- Article
- Export citation
A Numerical Lower Bound for the Spectral Radius of Random Walks on Surface Groups
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 6 / November 2015
- Published online by Cambridge University Press:
- 29 January 2015, pp. 838-856
-
- Article
- Export citation
Lazy Cops and Robbers on Hypercubes
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 6 / November 2015
- Published online by Cambridge University Press:
- 29 January 2015, pp. 829-837
-
- Article
- Export citation
On the Length of a Random Minimum Spanning Tree
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 23 January 2015, pp. 89-107
-
- Article
- Export citation