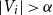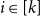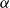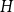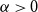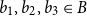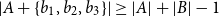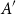Refine search
Actions for selected content:
6950 results in Algorithmics, Complexity, Computer Algebra, Computational Geometry
Conclusion
-
- Book:
- How to Think about Algorithms
- Published online:
- 10 October 2024
- Print publication:
- 07 March 2024, pp 588-588
-
- Chapter
- Export citation
Preface
-
- Book:
- How to Think about Algorithms
- Published online:
- 10 October 2024
- Print publication:
- 07 March 2024, pp xiii-xvi
-
- Chapter
- Export citation
Part III - Optimization Problems
-
- Book:
- How to Think about Algorithms
- Published online:
- 10 October 2024
- Print publication:
- 07 March 2024, pp 239-240
-
- Chapter
- Export citation
26 - The Game of Life
- from Part III - Optimization Problems
-
- Book:
- How to Think about Algorithms
- Published online:
- 10 October 2024
- Print publication:
- 07 March 2024, pp 380-389
-
- Chapter
- Export citation
14 - Recursive Images
- from Part II - Recursion
-
- Book:
- How to Think about Algorithms
- Published online:
- 10 October 2024
- Print publication:
- 07 March 2024, pp 192-197
-
- Chapter
- Export citation
5 - Categorical Duality
-
- Book:
- Topological Duality for Distributive Lattices
- Published online:
- 16 February 2024
- Print publication:
- 07 March 2024, pp 154-195
-
- Chapter
- Export citation
30 - Machine Learning
- from Part III - Optimization Problems
-
- Book:
- How to Think about Algorithms
- Published online:
- 10 October 2024
- Print publication:
- 07 March 2024, pp 431-438
-
- Chapter
- Export citation
38 - Adding-Made-Easy Approximations
- from Part IV - Additional Topics
-
- Book:
- How to Think about Algorithms
- Published online:
- 10 October 2024
- Print publication:
- 07 March 2024, pp 529-539
-
- Chapter
- Export citation
Antidirected subgraphs of oriented graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 06 March 2024, pp. 446-466
-
- Article
- Export citation
Large monochromatic components in expansive hypergraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 05 March 2024, pp. 467-483
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A class of graphs of zero Turán density in a hypercube
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 05 March 2024, pp. 404-410
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sharp bounds for a discrete John’s theorem
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 05 March 2024, pp. 484-486
-
- Article
- Export citation
Small subsets with large sumset: Beyond the Cauchy–Davenport bound
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 21 February 2024, pp. 411-431
-
- Article
- Export citation

Proven Impossible
- Elementary Proofs of Profound Impossibility from Arrow, Bell, Chaitin, Gödel, Turing and More
-
- Published online:
- 18 February 2024
- Print publication:
- 18 January 2024

Topological Duality for Distributive Lattices
- Theory and Applications
-
- Published online:
- 16 February 2024
- Print publication:
- 07 March 2024
On a conjecture of Conlon, Fox, and Wigderson
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 16 February 2024, pp. 432-445
-
- Article
- Export citation
Part I - Combinatorial Enumeration
-
- Book:
- Analytic Combinatorics in Several Variables
- Published online:
- 08 February 2024
- Print publication:
- 15 February 2024, pp 1-2
-
- Chapter
- Export citation
3 - Univariate asymptotics
- from Part I - Combinatorial Enumeration
-
- Book:
- Analytic Combinatorics in Several Variables
- Published online:
- 08 February 2024
- Print publication:
- 15 February 2024, pp 60-86
-
- Chapter
- Export citation
Appendix D - Stratification and stratified Morse theory
-
- Book:
- Analytic Combinatorics in Several Variables
- Published online:
- 08 February 2024
- Print publication:
- 15 February 2024, pp 513-532
-
- Chapter
- Export citation
Preface to the second edition
-
- Book:
- Analytic Combinatorics in Several Variables
- Published online:
- 08 February 2024
- Print publication:
- 15 February 2024, pp xi-xiii
-
- Chapter
- Export citation