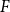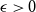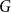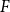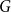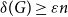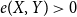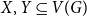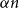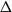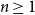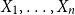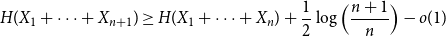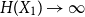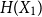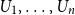Refine search
Actions for selected content:
6950 results in Algorithmics, Complexity, Computer Algebra, Computational Geometry
10 - Primal–Dual Technique
-
- Book:
- Online Algorithms
- Published online:
- 07 May 2024
- Print publication:
- 16 November 2023, pp 189-216
-
- Chapter
- Export citation
Appendix
-
- Book:
- Online Algorithms
- Published online:
- 07 May 2024
- Print publication:
- 16 November 2023, pp 433-438
-
- Chapter
- Export citation
6 - Metrical Task System
-
- Book:
- Online Algorithms
- Published online:
- 07 May 2024
- Print publication:
- 16 November 2023, pp 97-118
-
- Chapter
- Export citation
15 - Scheduling to Minimize Energy with Job Deadlines
-
- Book:
- Online Algorithms
- Published online:
- 07 May 2024
- Print publication:
- 16 November 2023, pp 329-360
-
- Chapter
- Export citation
Notation
-
- Book:
- Online Algorithms
- Published online:
- 07 May 2024
- Print publication:
- 16 November 2023, pp xxi-xxii
-
- Chapter
- Export citation
19 - Resource Constrained Scheduling (Energy Harvesting Communication)
-
- Book:
- Online Algorithms
- Published online:
- 07 May 2024
- Print publication:
- 16 November 2023, pp 409-420
-
- Chapter
- Export citation
Bibliography
-
- Book:
- Online Algorithms
- Published online:
- 07 May 2024
- Print publication:
- 16 November 2023, pp 439-462
-
- Chapter
- Export citation
Index
-
- Book:
- Online Algorithms
- Published online:
- 07 May 2024
- Print publication:
- 16 November 2023, pp 463-465
-
- Chapter
- Export citation
16 - Travelling Salesman
-
- Book:
- Online Algorithms
- Published online:
- 07 May 2024
- Print publication:
- 16 November 2023, pp 361-380
-
- Chapter
- Export citation
8 - Knapsack
-
- Book:
- Online Algorithms
- Published online:
- 07 May 2024
- Print publication:
- 16 November 2023, pp 139-160
-
- Chapter
- Export citation
Dedication
-
- Book:
- Online Algorithms
- Published online:
- 07 May 2024
- Print publication:
- 16 November 2023, pp v-vi
-
- Chapter
- Export citation
13 - Scheduling to Minimize Flow Time (Delay)
-
- Book:
- Online Algorithms
- Published online:
- 07 May 2024
- Print publication:
- 16 November 2023, pp 279-304
-
- Chapter
- Export citation
12 - Load Balancing
-
- Book:
- Online Algorithms
- Published online:
- 07 May 2024
- Print publication:
- 16 November 2023, pp 247-278
-
- Chapter
- Export citation
14 - Scheduling with Speed Scaling
-
- Book:
- Online Algorithms
- Published online:
- 07 May 2024
- Print publication:
- 16 November 2023, pp 305-328
-
- Chapter
- Export citation
5 - Paging
-
- Book:
- Online Algorithms
- Published online:
- 07 May 2024
- Print publication:
- 16 November 2023, pp 67-96
-
- Chapter
- Export citation
Large cliques or cocliques in hypergraphs with forbidden order-size pairs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 16 November 2023, pp. 286-299
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
17 - Convex Optimization (Server Provisioning in Cloud Computing)
-
- Book:
- Online Algorithms
- Published online:
- 07 May 2024
- Print publication:
- 16 November 2023, pp 381-396
-
- Chapter
- Export citation
3 - List Accessing
-
- Book:
- Online Algorithms
- Published online:
- 07 May 2024
- Print publication:
- 16 November 2023, pp 27-48
-
- Chapter
- Export citation
Spanning trees in graphs without large bipartite holes
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 14 November 2023, pp. 270-285
-
- Article
-
- You have access
- HTML
- Export citation
Approximate discrete entropy monotonicity for log-concave sums
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 13 November 2023, pp. 196-209
-
- Article
- Export citation