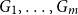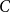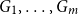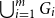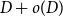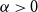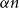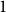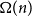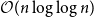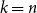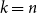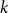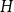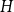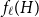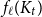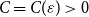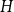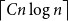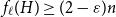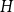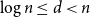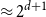Refine search
Actions for selected content:
6950 results in Algorithmics, Complexity, Computer Algebra, Computational Geometry
A special case of Vu’s conjecture: colouring nearly disjoint graphs of bounded maximum degree
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 10 November 2023, pp. 179-195
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On oriented cycles in randomly perturbed digraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 08 November 2023, pp. 157-178
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mastermind with a linear number of queries
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 08 November 2023, pp. 143-156
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the choosability of
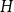 $H$-minor-free graphs
$H$-minor-free graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 03 November 2023, pp. 129-142
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Spanning subdivisions in Dirac graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 20 October 2023, pp. 121-128
-
- Article
- Export citation
Many Hamiltonian subsets in large graphs with given density
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 02 October 2023, pp. 110-120
-
- Article
- Export citation
Intersecting families without unique shadow
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 02 October 2023, pp. 91-109
-
- Article
- Export citation
3 - Common Discrete Random Variables
- from Part II - Discrete Random Variables
-
- Book:
- Introduction to Probability for Computing
- Published online:
- 12 September 2023
- Print publication:
- 28 September 2023, pp 44-57
-
- Chapter
- Export citation
15 - Estimators for Mean and Variance
- from Part V - Statistical Inference
-
- Book:
- Introduction to Probability for Computing
- Published online:
- 12 September 2023
- Print publication:
- 28 September 2023, pp 255-264
-
- Chapter
- Export citation
References
-
- Book:
- Introduction to Probability for Computing
- Published online:
- 12 September 2023
- Print publication:
- 28 September 2023, pp 539-543
-
- Chapter
- Export citation
Copyright page
-
- Book:
- Introduction to Probability for Computing
- Published online:
- 12 September 2023
- Print publication:
- 28 September 2023, pp iv-iv
-
- Chapter
- Export citation
12 - The Poisson Process
- from Part IV - Computer Systems Modeling and Simulation
-
- Book:
- Introduction to Probability for Computing
- Published online:
- 12 September 2023
- Print publication:
- 28 September 2023, pp 210-228
-
- Chapter
- Export citation
24 - Discrete-Time Markov Chains: Finite-State
- from Part VIII - Discrete-Time Markov Chains
-
- Book:
- Introduction to Probability for Computing
- Published online:
- 12 September 2023
- Print publication:
- 28 September 2023, pp 420-437
-
- Chapter
- Export citation
20 - Hashing Algorithms
- from Part VI - Tail Bounds and Applications
-
- Book:
- Introduction to Probability for Computing
- Published online:
- 12 September 2023
- Print publication:
- 28 September 2023, pp 346-362
-
- Chapter
- Export citation
Part VII - Randomized Algorithms
-
- Book:
- Introduction to Probability for Computing
- Published online:
- 12 September 2023
- Print publication:
- 28 September 2023, pp 363-418
-
- Chapter
- Export citation
8 - Continuous Random Variables: Joint Distributions
- from Part III - Continuous Random Variables
-
- Book:
- Introduction to Probability for Computing
- Published online:
- 12 September 2023
- Print publication:
- 28 September 2023, pp 153-169
-
- Chapter
- Export citation
Part VIII - Discrete-Time Markov Chains
-
- Book:
- Introduction to Probability for Computing
- Published online:
- 12 September 2023
- Print publication:
- 28 September 2023, pp 419-538
-
- Chapter
- Export citation
10 - Heavy Tails: The Distributions of Computing
- from Part III - Continuous Random Variables
-
- Book:
- Introduction to Probability for Computing
- Published online:
- 12 September 2023
- Print publication:
- 28 September 2023, pp 181-197
-
- Chapter
- Export citation
Preface
-
- Book:
- Introduction to Probability for Computing
- Published online:
- 12 September 2023
- Print publication:
- 28 September 2023, pp xv-xxi
-
- Chapter
- Export citation
Dedication
-
- Book:
- Introduction to Probability for Computing
- Published online:
- 12 September 2023
- Print publication:
- 28 September 2023, pp v-vi
-
- Chapter
- Export citation