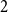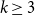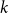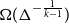Refine search
Actions for selected content:
6950 results in Algorithmics, Complexity, Computer Algebra, Computational Geometry
11 - Polynomials with real coefficients
- from Part III - Polynomials
-
- Book:
- Graph Spectra for Complex Networks
- Published online:
- 07 September 2023
- Print publication:
- 21 September 2023, pp 401-466
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Graph Spectra for Complex Networks
- Published online:
- 07 September 2023
- Print publication:
- 21 September 2023, pp i-iv
-
- Chapter
- Export citation
Bibliography
-
- Book:
- Graph Spectra for Complex Networks
- Published online:
- 07 September 2023
- Print publication:
- 21 September 2023, pp 503-512
-
- Chapter
- Export citation
5 - Effective resistance matrix
- from Part I - Spectra of graphs
-
- Book:
- Graph Spectra for Complex Networks
- Published online:
- 07 September 2023
- Print publication:
- 21 September 2023, pp 175-192
-
- Chapter
- Export citation
Part III - Polynomials
-
- Book:
- Graph Spectra for Complex Networks
- Published online:
- 07 September 2023
- Print publication:
- 21 September 2023, pp 399-400
-
- Chapter
- Export citation
10 - Eigensystem of a matrix
- from Part II - Eigensystem
-
- Book:
- Graph Spectra for Complex Networks
- Published online:
- 07 September 2023
- Print publication:
- 21 September 2023, pp 345-398
-
- Chapter
- Export citation
On the zeroes of hypergraph independence polynomials
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 21 September 2023, pp. 65-84
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Preface to the first edition
-
- Book:
- Graph Spectra for Complex Networks
- Published online:
- 07 September 2023
- Print publication:
- 21 September 2023, pp xiii-xv
-
- Chapter
- Export citation
3 - Eigenvalues of the adjacency matrix
- from Part I - Spectra of graphs
-
- Book:
- Graph Spectra for Complex Networks
- Published online:
- 07 September 2023
- Print publication:
- 21 September 2023, pp 51-110
-
- Chapter
- Export citation
6 - Spectra of special types of graphs
- from Part I - Spectra of graphs
-
- Book:
- Graph Spectra for Complex Networks
- Published online:
- 07 September 2023
- Print publication:
- 21 September 2023, pp 193-246
-
- Chapter
- Export citation
Preface to the second edition
-
- Book:
- Graph Spectra for Complex Networks
- Published online:
- 07 September 2023
- Print publication:
- 21 September 2023, pp xi-xii
-
- Chapter
- Export citation
12 - Orthogonal polynomials
- from Part III - Polynomials
-
- Book:
- Graph Spectra for Complex Networks
- Published online:
- 07 September 2023
- Print publication:
- 21 September 2023, pp 467-502
-
- Chapter
- Export citation
4 - Eigenvalues of the Laplacian Q
- from Part I - Spectra of graphs
-
- Book:
- Graph Spectra for Complex Networks
- Published online:
- 07 September 2023
- Print publication:
- 21 September 2023, pp 111-174
-
- Chapter
- Export citation
2 - Algebraic graph theory
- from Part I - Spectra of graphs
-
- Book:
- Graph Spectra for Complex Networks
- Published online:
- 07 September 2023
- Print publication:
- 21 September 2023, pp 15-50
-
- Chapter
- Export citation
Acknowledgements
-
- Book:
- Graph Spectra for Complex Networks
- Published online:
- 07 September 2023
- Print publication:
- 21 September 2023, pp xvi-xvi
-
- Chapter
- Export citation
Contents
-
- Book:
- Graph Spectra for Complex Networks
- Published online:
- 07 September 2023
- Print publication:
- 21 September 2023, pp vii-x
-
- Chapter
- Export citation
Height function localisation on trees
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 18 September 2023, pp. 50-64
-
- Article
-
- You have access
- Open access
- HTML
- Export citation

Introduction to Probability for Computing
-
- Published online:
- 12 September 2023
- Print publication:
- 28 September 2023
-
- Textbook
- Export citation
On the size of maximal intersecting families
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 08 September 2023, pp. 32-49
-
- Article
- Export citation

Graph Spectra for Complex Networks
-
- Published online:
- 07 September 2023
- Print publication:
- 21 September 2023