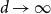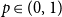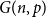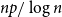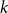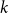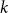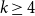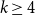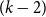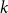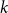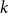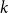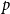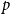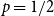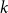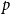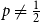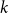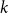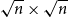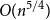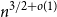Refine search
Actions for selected content:
6950 results in Algorithmics, Complexity, Computer Algebra, Computational Geometry
On the exponential growth rates of lattice animals and interfaces
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 31 July 2023, pp. 912-955
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Limiting empirical spectral distribution for the non-backtracking matrix of an Erdős-Rényi random graph
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 31 July 2023, pp. 956-973
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the maximum number of edges in
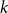 $k$-critical graphs
$k$-critical graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 24 July 2023, pp. 900-911
-
- Article
- Export citation
Polarised random
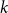 $k$-SAT
$k$-SAT
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 20 July 2023, pp. 885-899
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The codegree Turán density of tight cycles minus one edge
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 05 July 2023, pp. 881-884
-
- Article
-
- You have access
- Open access
- HTML
- Export citation

Descriptive vs. Inferential Community Detection in Networks
- Pitfalls, Myths and Half-Truths
-
- Published online:
- 04 July 2023
- Print publication:
- 31 August 2023
-
- Element
-
- You have access
- Open access
- HTML
- Export citation
On the size-Ramsey number of grids
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 26 June 2023, pp. 874-880
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Chapter Twenty - Unraveling
- from Part Three - Theory
-
- Book:
- Online and Matching-Based Market Design
- Published online:
- 13 May 2023
- Print publication:
- 22 June 2023, pp 428-447
-
- Chapter
- Export citation
11 - Integer Coding
-
- Book:
- Pearls of Algorithm Engineering
- Published online:
- 08 June 2023
- Print publication:
- 22 June 2023, pp 194-209
-
- Chapter
- Export citation
Chapter Fifteen - Complementarities and Externalities
- from Part Three - Theory
-
- Book:
- Online and Matching-Based Market Design
- Published online:
- 13 May 2023
- Print publication:
- 22 June 2023, pp 323-342
-
- Chapter
- Export citation
10 - Complex Numbers
-
- Book:
- Introduction to Proofs and Proof Strategies
- Published online:
- 08 June 2023
- Print publication:
- 22 June 2023, pp 266-305
-
- Chapter
- Export citation
Part Four - Empirics
-
- Book:
- Online and Matching-Based Market Design
- Published online:
- 13 May 2023
- Print publication:
- 22 June 2023, pp 509-510
-
- Chapter
- Export citation
4 - List Ranking
-
- Book:
- Pearls of Algorithm Engineering
- Published online:
- 08 June 2023
- Print publication:
- 22 June 2023, pp 32-43
-
- Chapter
- Export citation
2 - A Warm-up
-
- Book:
- Pearls of Algorithm Engineering
- Published online:
- 08 June 2023
- Print publication:
- 22 June 2023, pp 10-22
-
- Chapter
- Export citation
Contents
-
- Book:
- Online and Matching-Based Market Design
- Published online:
- 13 May 2023
- Print publication:
- 22 June 2023, pp v-xii
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Online and Matching-Based Market Design
- Published online:
- 13 May 2023
- Print publication:
- 22 June 2023, pp i-iv
-
- Chapter
- Export citation
Chapter Five - Applications of Online Matching
- from Part Two - Applications (Modern and Traditional)
-
- Book:
- Online and Matching-Based Market Design
- Published online:
- 13 May 2023
- Print publication:
- 22 June 2023, pp 109-129
-
- Chapter
- Export citation
1 - Introduction
-
- Book:
- Pearls of Algorithm Engineering
- Published online:
- 08 June 2023
- Print publication:
- 22 June 2023, pp 1-9
-
- Chapter
- Export citation
Chapter One - Two-Sided Markets: Stable Matching
- from Part One - Foundations of Market Design
-
- Book:
- Online and Matching-Based Market Design
- Published online:
- 13 May 2023
- Print publication:
- 22 June 2023, pp 3-36
-
- Chapter
- Export citation
Chapter Twenty-Two - Signaling in Two-Sided Matching Markets
- from Part Three - Theory
-
- Book:
- Online and Matching-Based Market Design
- Published online:
- 13 May 2023
- Print publication:
- 22 June 2023, pp 467-483
-
- Chapter
- Export citation