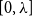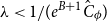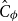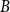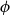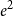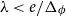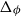Refine search
Actions for selected content:
6950 results in Algorithmics, Complexity, Computer Algebra, Computational Geometry
Forcing generalised quasirandom graphs efficiently
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 05 September 2023, pp. 16-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Frontmatter
-
- Book:
- Graph Theory and Additive Combinatorics
- Published online:
- 10 August 2023
- Print publication:
- 31 August 2023, pp i-iv
-
- Chapter
- Export citation
4 - Graph Limits
-
- Book:
- Graph Theory and Additive Combinatorics
- Published online:
- 10 August 2023
- Print publication:
- 31 August 2023, pp 127-157
-
- Chapter
- Export citation
Notation and Conventions
-
- Book:
- Graph Theory and Additive Combinatorics
- Published online:
- 10 August 2023
- Print publication:
- 31 August 2023, pp xv-xviii
-
- Chapter
- Export citation
5 - Graph Homomorphism Inequalities
-
- Book:
- Graph Theory and Additive Combinatorics
- Published online:
- 10 August 2023
- Print publication:
- 31 August 2023, pp 158-196
-
- Chapter
- Export citation
9 - Progressions in Sparse Pseudorandom Sets
-
- Book:
- Graph Theory and Additive Combinatorics
- Published online:
- 10 August 2023
- Print publication:
- 31 August 2023, pp 273-296
-
- Chapter
- Export citation
6 - Forbidding 3-Term Arithmetic Progressions
-
- Book:
- Graph Theory and Additive Combinatorics
- Published online:
- 10 August 2023
- Print publication:
- 31 August 2023, pp 197-229
-
- Chapter
- Export citation
Contents
-
- Book:
- Graph Theory and Additive Combinatorics
- Published online:
- 10 August 2023
- Print publication:
- 31 August 2023, pp vii-x
-
- Chapter
- Export citation
0 - Appetizer: Triangles and Equations
-
- Book:
- Graph Theory and Additive Combinatorics
- Published online:
- 10 August 2023
- Print publication:
- 31 August 2023, pp 1-10
-
- Chapter
- Export citation
Index
-
- Book:
- Graph Theory and Additive Combinatorics
- Published online:
- 10 August 2023
- Print publication:
- 31 August 2023, pp 313-316
-
- Chapter
- Export citation
7 - Structure of Set Addition
-
- Book:
- Graph Theory and Additive Combinatorics
- Published online:
- 10 August 2023
- Print publication:
- 31 August 2023, pp 230-263
-
- Chapter
- Export citation
8 - Sum-Product Problem
-
- Book:
- Graph Theory and Additive Combinatorics
- Published online:
- 10 August 2023
- Print publication:
- 31 August 2023, pp 264-272
-
- Chapter
- Export citation
1 - Forbidding a Subgraph
-
- Book:
- Graph Theory and Additive Combinatorics
- Published online:
- 10 August 2023
- Print publication:
- 31 August 2023, pp 11-51
-
- Chapter
- Export citation
References
-
- Book:
- Graph Theory and Additive Combinatorics
- Published online:
- 10 August 2023
- Print publication:
- 31 August 2023, pp 297-312
-
- Chapter
- Export citation
Preface
-
- Book:
- Graph Theory and Additive Combinatorics
- Published online:
- 10 August 2023
- Print publication:
- 31 August 2023, pp xi-xiv
-
- Chapter
- Export citation
Dedication
-
- Book:
- Graph Theory and Additive Combinatorics
- Published online:
- 10 August 2023
- Print publication:
- 31 August 2023, pp v-vi
-
- Chapter
- Export citation
3 - Pseudorandom Graphs
-
- Book:
- Graph Theory and Additive Combinatorics
- Published online:
- 10 August 2023
- Print publication:
- 31 August 2023, pp 89-126
-
- Chapter
- Export citation
2 - Graph Regularity Method
-
- Book:
- Graph Theory and Additive Combinatorics
- Published online:
- 10 August 2023
- Print publication:
- 31 August 2023, pp 52-88
-
- Chapter
- Export citation
Quasipolynomial-time algorithms for Gibbs point processes
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 11 August 2023, pp. 1-15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation

Graph Theory and Additive Combinatorics
- Exploring Structure and Randomness
-
- Published online:
- 10 August 2023
- Print publication:
- 31 August 2023