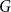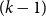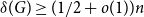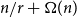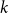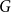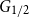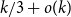Skip to main content Accessibility help
×
  1. Home
  2. Browse subjects
  3. Computer Science
  4. Algorithmics, Complexity, Computer Algebra, Computational Geometry
  5. Content listing

Refine search

Refine search

Access:
Content type:
Publication date:
Apply   From and To filters
Subject: Show more
Journals Show more
Publishers: Show more
Societies Show more
Series: Show more
Collections: Show more

Actions for selected content:

Select all | Deselect all
  • View selected items
  • Export citations
  • Download PDF (zip)
  • Save to Kindle
  • Save to Dropbox
  • Save to Google Drive

Save Search

You can save your searches here and later view and run them again in "My saved searches".

Please provide a title, maximum of 40 characters.
Cancel
×

6950 results in Algorithmics, Complexity, Computer Algebra, Computational Geometry

Page 5 of 348

  • 10 - Further Research

  • Jan Krajíček, Charles University, Prague
  • Book:
    Proof Complexity Generators
    Published online:
    29 May 2025
    Print publication:
    26 June 2025, pp 104-110

  • Summary

    This final chapter offers a number of topics for further research involving ordinary PHP, S-T computations, a new notion of PLS-infinite NP sets, proof search algorithms, an exponential time weakening of generators and the function inversion problem.

  • 7 - The Case of ER

  • Jan Krajíček, Charles University, Prague
  • Book:
    Proof Complexity Generators
    Published online:
    29 May 2025
    Print publication:
    26 June 2025, pp 58-74

  • Summary

    The chapter concentrates on the pivotal case of extended resolution. It recalls some characterizations of its lengths-of-proofs function and formulates a framework for lower bounds proofs using expansions of pseudofinite structures. It gives an example of a specific candidate construction.

  • 9 - Contexts

  • Jan Krajíček, Charles University, Prague
  • Book:
    Proof Complexity Generators
    Published online:
    29 May 2025
    Print publication:
    26 June 2025, pp 93-103

  • Summary

    The chapter presents several topics outside of the theory where some ideas and results around proof complexity generators appear to be relevant. These include SAT algorithms, the optimality problem of proof complexity, structured PHP approach, the incompleteness theorem and total NP search problems.

  • On the size of temporal cliques in subcritical random temporal graphs

  • Part of
  • Caelan Atamanchuk, Luc Devroye, Gábor Lugosi
  • Journal:
    Combinatorics, Probability and Computing / Volume 34 / Issue 5 / September 2025
    Published online by Cambridge University Press:
    26 June 2025, pp. 671-679

  • A random temporal graph is an Erdős-Rényi random graph $G(n,p)$, together with a random ordering of its edges. A path in the graph is called increasing if the edges on the path appear in increasing order. A set $S$ of vertices forms a temporal clique if for all $u,v \in S$, there is an increasing path from $u$ to $v$. Becker, Casteigts, Crescenzi, Kodric, Renken, Raskin and Zamaraev [(2023) Giant components in random temporal graphs. arXiv,2205.14888] proved that if $p=c\log n/n$ for $c\gt 1$, then, with high probability, there is a temporal clique of size $n-o(n)$. On the other hand, for $c\lt 1$, with high probability, the largest temporal clique is of size $o(n)$. In this note, we improve the latter bound by showing that, for $c\lt 1$, the largest temporal clique is of constant size with high probability.

  • 4 - The Stretch

  • Jan Krajíček, Charles University, Prague
  • Book:
    Proof Complexity Generators
    Published online:
    29 May 2025
    Print publication:
    26 June 2025, pp 30-41

  • Summary

    The chapter examines possible stretch of generators and relates it to problems about Kolmogorov's complexity, the feasible disjunction property and to a related notion of disjunction hardness of generators. The truth-table function is presented as a key example of a generator and its hardness and pseudosurjectivity is considered. A problem about time-bounded Kolmogorov complexity is formulated.

Oriented Matroids
  • Laura Anderson
  • Published online:
    04 June 2025
    Print publication:
    10 April 2025
  • Oriented matroids appear throughout discrete geometry, with applications in algebra, topology, physics, and data analysis. This introduction to oriented matroids is intended for graduate students, scientists wanting to apply oriented matroids, and researchers in pure mathematics. The presentation is geometrically motivated and largely self-contained, and no knowledge of matroid theory is assumed. Beginning with geometric motivation grounded in linear algebra, the first chapters prove the major cryptomorphisms and the Topological Representation Theorem. From there the book uses basic topology to go directly from geometric intuition to rigorous discussion, avoiding the need for wider background knowledge. Topics include strong and weak maps, localizations and extensions, the Euclidean property and non-Euclidean properties, the Universality Theorem, convex polytopes, and triangulations. Themes that run throughout include the interplay between combinatorics, geometry, and topology, and the idea of oriented matroids as analogs to vector spaces over the real numbers and how this analogy plays out topologically.

Games of No Chance 4
  • Edited by Richard J. Nowakowski
  • Mathematical Sciences Research Institute
  • Published online:
    30 May 2025
    Print publication:
    16 April 2015
  • Combinatorial games are the strategy games that people like to play, for example chess, Hex, and Go. They differ from economic games in that there are two players who play alternately with no hidden cards and no dice. These games have a mathematical structure that allows players to analyse them in the abstract. Games of No Chance 4 contains the first comprehensive explorations of misère (last player to move loses) games, extends the theory for some classes of normal-play (last player to move wins) games and extends the analysis for some specific games. It includes a tutorial for the very successful approach to analysing misère impartial games and the first attempt at using it for misère partisan games. Hex and Go are featured, as well as new games: Toppling Dominoes and Maze. Updated versions of Unsolved Problems in Combinatorial Game Theory and the Combinatorial Games Bibliography complete the volume.

Algorithmic Number Theory
  • Lattices, Number Fields, Curves and Cryptography
  • Edited by J. P. Buhler, P. Stevenhagen
  • Mathematical Sciences Research Institute
  • Published online:
    30 May 2025
    Print publication:
    20 October 2008
  • Number theory is one of the oldest and most appealing areas of mathematics. Computation has always played a role in number theory, a role which has increased dramatically in the last 20 or 30 years, both because of the advent of modern computers, and because of the discovery of surprising and powerful algorithms. As a consequence, algorithmic number theory has gradually emerged as an important and distinct field with connections to computer science and cryptography as well as other areas of mathematics. This text provides a comprehensive introduction to algorithmic number theory for beginning graduate students, written by the leading experts in the field. It includes several articles that cover the essential topics in this area, and in addition, there are contributions pointing in broader directions, including cryptography, computational class field theory, zeta functions and L-series, discrete logarithm algorithms, and quantum computing.

  • Tight Hamilton cycles with high discrepancy

  • Part of
  • Lior Gishboliner, Stefan Glock, Amedeo Sgueglia
  • Journal:
    Combinatorics, Probability and Computing / Volume 34 / Issue 4 / July 2025
    Published online by Cambridge University Press:
    30 May 2025, pp. 565-584
    • Article
      • You have access
      • Open access
    • PDF
    • HTML
    • Export citation

  • In this paper, we study discrepancy questions for spanning subgraphs of $k$-uniform hypergraphs. Our main result is that, for any integers $k \ge 3$ and $r \ge 2$, any $r$-colouring of the edges of a $k$-uniform $n$-vertex hypergraph $G$ with minimum $(k-1)$-degree $\delta (G) \ge (1/2+o(1))n$ contains a tight Hamilton cycle with high discrepancy, that is, with at least $n/r+\Omega (n)$ edges of one colour. The minimum degree condition is asymptotically best possible and our theorem also implies a corresponding result for perfect matchings. Our tools combine various structural techniques such as Turán-type problems and hypergraph shadows with probabilistic techniques such as random walks and the nibble method. We also propose several intriguing problems for future research.

More Games of No Chance
  • Edited by Richard Nowakowski
  • Mathematical Sciences Research Institute
  • Published online:
    29 May 2025
    Print publication:
    25 November 2002
  • This 2003 book provides an analysis of combinatorial games - games not involving chance or hidden information. It contains a fascinating collection of articles by some well-known names in the field, such as Elwyn Berlekamp and John Conway, plus other researchers in mathematics and computer science, together with some top game players. The articles run the gamut from theoretical approaches (infinite games, generalizations of game values, 2-player cellular automata, Alpha-Beta pruning under partial orders) to other games (Amazons, Chomp, Dot-and-Boxes, Go, Chess, Hex). Many of these advances reflect the interplay of the computer science and the mathematics. The book ends with a bibliography by A. Fraenkel and a list of combinatorial game theory problems by R. K. Guy. Like its predecessor, Games of No Chance, this should be on the shelf of all serious combinatorial games enthusiasts.

Proof Complexity Generators
  • Jan Krajíček
  • Published online:
    29 May 2025
    Print publication:
    26 June 2025
  • The P vs. NP problem is one of the fundamental problems of mathematics. It asks whether propositional tautologies can be recognized by a polynomial-time algorithm. The problem would be solved in the negative if one could show that there are propositional tautologies that are very hard to prove, no matter how powerful the proof system you use. This is the foundational problem (the NP vs. coNP problem) of proof complexity, an area linking mathematical logic and computational complexity theory. Written by a leading expert in the field, this book presents a theory for constructing such hard tautologies. It introduces the theory step by step, starting with the historic background and a motivational problem in bounded arithmetic, before taking the reader on a tour of various vistas of the field. Finally, it formulates several research problems to highlight new avenues of research.

  • Short proof of the hypergraph container theorem

  • Part of
  • Rajko Nenadov, Huy Tuan Pham
  • Journal:
    Combinatorics, Probability and Computing / Volume 34 / Issue 5 / September 2025
    Published online by Cambridge University Press:
    16 May 2025, pp. 621-624

  • We present a short and simple proof of the celebrated hypergraph container theorem of Balogh–Morris–Samotij and Saxton–Thomason. On a high level, our argument utilises the idea of iteratively taking vertices of largest degree from an independent set and constructing a hypergraph of lower uniformity which preserves independent sets and inherits edge distribution. The original algorithms for constructing containers also remove in each step vertices of high degree, which are not in the independent set. Our modified algorithm postpones this until the end, which surprisingly results in a significantly simplified analysis.

Quantum Algorithms
  • A Survey of Applications and End-to-end Complexities
  • Alexander M. Dalzell, Sam McArdle, Mario Berta, Przemyslaw Bienias, Chi-Fang Chen, András Gilyén, Connor T. Hann, Michael J. Kastoryano, Emil T. Khabiboulline, Aleksander Kubica, Grant Salton, Samson Wang, Fernando G. S. L. Brandão
  • Published online:
    03 May 2025
    Print publication:
    24 April 2025
  • The 1994 discovery of Shor's quantum algorithm for integer factorization—an important practical problem in the area of cryptography—demonstrated quantum computing's potential for real-world impact. Since then, researchers have worked intensively to expand the list of practical problems that quantum algorithms can solve effectively. This book surveys the fruits of this effort, covering proposed quantum algorithms for concrete problems in many application areas, including quantum chemistry, optimization, finance, and machine learning. For each quantum algorithm considered, the book clearly states the problem being solved and the full computational complexity of the procedure, making sure to account for the contribution from all the underlying primitive ingredients. Separately, the book provides a detailed, independent summary of the most common algorithmic primitives. It has a modular, encyclopedic format to facilitate navigation of the material and to provide a quick reference for designers of quantum algorithms and quantum computing researchers.
An Introduction to String Diagrams for Computer Scientists

An Introduction to String Diagrams for Computer Scientists
  • Robin Piedeleu, Fabio Zanasi
  • Published online:
    01 May 2025
    Print publication:
    29 May 2025
    • Element
      • You have access
      • Open access
    • PDF
    • HTML
    • Export citation
  • String diagrams are a powerful graphical language used to represent computational phenomena across diverse scientific fields, including computer science, physics, linguistics, amongst others. The appeal of string diagrams lies in their multi-faceted nature: they offer a simple, visual representation of complex scientific ideas, while also allowing rigorous mathematical treatment. Originating in category theory, string diagrams have since evolved into a versatile formalism, extending well beyond their abstract algebraic roots, and offering alternative entry points to their study. This text provides an accessible introduction to string diagrams from the perspective of computer science. Rather than starting from categorical concepts, the authors draw on intuitions from formal language theory, treating string diagrams as a syntax with its own semantics. They survey the basic theory, outline fundamental principles, and highlight modern applications of string diagrams in different fields. This title is also available as open access on Cambridge Core.

Data Structures and Algorithms Using Python
  • Subrata Saha
  • Published online:
    30 April 2025
    Print publication:
    15 June 2023
  • Efficiently using data structures to collect, organise and retrieve information is one of the core abilities modern computer engineers are expected to have. This student-friendly textbook provides a complete view of data structures and algorithms using the Python programming language, striking a balance between theory and practical application. All major algorithms have been discussed and analysed in detail, and the corresponding codes in Python have been provided. Diagrams and examples have been extensively used for better understanding. Running time complexities are also discussed for each algorithm, allowing the student to better understand how to select the appropriate one. Written with both undergraduate and graduate students in mind, the book will also be helpful with competitive examinations for engineering in India such as GATE and NET. As such, it will be a vital resource for students as well as professionals who are looking for a handbook on data structures in Python.

  • Colouring random subgraphs

  • Part of
  • Boris Bukh, Michael Krivelevich, Bhargav Narayanan
  • Journal:
    Combinatorics, Probability and Computing / Volume 34 / Issue 4 / July 2025
    Published online by Cambridge University Press:
    28 April 2025, pp. 585-595

  • We study several basic problems about colouring the $p$-random subgraph $G_p$ of an arbitrary graph $G$, focusing primarily on the chromatic number and colouring number of $G_p$. In particular, we show that there exist infinitely many $k$-regular graphs $G$ for which the colouring number (i.e., degeneracy) of $G_{1/2}$ is at most $k/3 + o(k)$ with high probability, thus disproving the natural prediction that such random graphs must have colouring number at least $k/2 - o(k)$.

  • 17 - Loading classical data

  • from Part II - Quantum algorithmic primitives
  • Alexander M. Dalzell, AWS Center for Quantum Computing, Sam McArdle, AWS Center for Quantum Computing, Mario Berta, RWTH Aachen University, Przemyslaw Bienias, AWS Center for Quantum Computing, Chi-Fang Chen, University of California, Berkeley, András Gilyén, HUN-REN Alfréd Rényi Institute of Mathematics, Connor T. Hann, AWS Center for Quantum Computing, Michael J. Kastoryano, University of Copenhagen, Emil T. Khabiboulline, National Institute of Standards and Technology, Aleksander Kubica, Yale University, Grant Salton, Amazon Quantum Solutions Lab, Samson Wang, Caltech, Fernando G. S. L. Brandão, AWS Center for Quantum Computing
  • Book:
    Quantum Algorithms
    Published online:
    03 May 2025
    Print publication:
    24 April 2025, pp 255-269
    • Chapter
      • You have access
      • Open access
    • PDF
    • Export citation

  • Summary

    This chapter covers quantum algorithmic primitives for loading classical data into a quantum algorithm. These primitives are important in many quantum algorithms, and they are especially essential for algorithms for big-data problems in the area of machine learning. We cover quantum random access memory (QRAM), an operation that allows a quantum algorithm to query a classical database in superposition. We carefully detail caveats and nuances that appear for realizing fast large-scale QRAM and what this means for algorithms that rely upon QRAM. We also cover primitives for preparing arbitrary quantum states given a list of the amplitudes stored in a classical database, and for performing a block-encoding of a matrix, given a list of its entries stored in a classical database.

Page 5 of 348