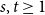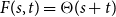Refine search
Actions for selected content:
6950 results in Algorithmics, Complexity, Computer Algebra, Computational Geometry
5 - Strong Maps and Weak Maps
-
- Book:
- Oriented Matroids
- Published online:
- 04 June 2025
- Print publication:
- 10 April 2025, pp 136-157
-
- Chapter
- Export citation
8 - Oriented Matroid Polytopes
-
- Book:
- Oriented Matroids
- Published online:
- 04 June 2025
- Print publication:
- 10 April 2025, pp 242-257
-
- Chapter
- Export citation
Preface
-
- Book:
- Oriented Matroids
- Published online:
- 04 June 2025
- Print publication:
- 10 April 2025, pp xi-xii
-
- Chapter
- Export citation
Contents
-
- Book:
- Oriented Matroids
- Published online:
- 04 June 2025
- Print publication:
- 10 April 2025, pp vii-x
-
- Chapter
- Export citation
3 - Elementary Operations and Properties
-
- Book:
- Oriented Matroids
- Published online:
- 04 June 2025
- Print publication:
- 10 April 2025, pp 92-102
-
- Chapter
- Export citation
Dedication
-
- Book:
- Oriented Matroids
- Published online:
- 04 June 2025
- Print publication:
- 10 April 2025, pp v-vi
-
- Chapter
- Export citation
Index
-
- Book:
- Oriented Matroids
- Published online:
- 04 June 2025
- Print publication:
- 10 April 2025, pp 317-322
-
- Chapter
- Export citation
6 - Single-Element Extensions
-
- Book:
- Oriented Matroids
- Published online:
- 04 June 2025
- Print publication:
- 10 April 2025, pp 158-213
-
- Chapter
- Export citation
References
-
- Book:
- Oriented Matroids
- Published online:
- 04 June 2025
- Print publication:
- 10 April 2025, pp 310-316
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Oriented Matroids
- Published online:
- 04 June 2025
- Print publication:
- 10 April 2025, pp i-iv
-
- Chapter
- Export citation
9 - Subdivisions and Triangulations
-
- Book:
- Oriented Matroids
- Published online:
- 04 June 2025
- Print publication:
- 10 April 2025, pp 258-295
-
- Chapter
- Export citation
4 - The Topological Representation Theorem
-
- Book:
- Oriented Matroids
- Published online:
- 04 June 2025
- Print publication:
- 10 April 2025, pp 103-135
-
- Chapter
- Export citation
Hamiltonicity of sparse pseudorandom graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 4 / July 2025
- Published online by Cambridge University Press:
- 25 March 2025, pp. 596-620
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A note on digraph splitting
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 4 / July 2025
- Published online by Cambridge University Press:
- 21 March 2025, pp. 559-564
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Face enumeration for split matroid polytopes
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 4 / July 2025
- Published online by Cambridge University Press:
- 07 February 2025, pp. 528-544
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
7 - Terminal Coalgebras as Algebras, Initial Algebras as Coalgebras
-
- Book:
- Initial Algebras and Terminal Coalgebras
- Published online:
- 30 January 2025
- Print publication:
- 06 February 2025, pp 215-252
-
- Chapter
- Export citation
8 - Well-Founded Coalgebras
-
- Book:
- Initial Algebras and Terminal Coalgebras
- Published online:
- 30 January 2025
- Print publication:
- 06 February 2025, pp 253-292
-
- Chapter
- Export citation
11 - Sufficient Conditions for Initial Algebras and Terminal Coalgebras
-
- Book:
- Initial Algebras and Terminal Coalgebras
- Published online:
- 30 January 2025
- Print publication:
- 06 February 2025, pp 363-397
-
- Chapter
- Export citation
Preface
-
- Book:
- Initial Algebras and Terminal Coalgebras
- Published online:
- 30 January 2025
- Print publication:
- 06 February 2025, pp xi-xiv
-
- Chapter
- Export citation
Contents
-
- Book:
- Initial Algebras and Terminal Coalgebras
- Published online:
- 30 January 2025
- Print publication:
- 06 February 2025, pp vii-x
-
- Chapter
- Export citation