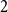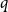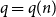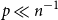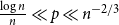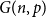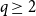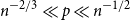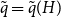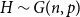Refine search
Actions for selected content:
6950 results in Algorithmics, Complexity, Computer Algebra, Computational Geometry
Index
-
- Book:
- Approximation Algorithms for Traveling Salesman Problems
- Published online:
- 14 November 2024
- Print publication:
- 05 December 2024, pp 423-428
-
- Chapter
- Export citation
16 - Path TSP by Dynamic Programming
-
- Book:
- Approximation Algorithms for Traveling Salesman Problems
- Published online:
- 14 November 2024
- Print publication:
- 05 December 2024, pp 351-380
-
- Chapter
- Export citation
12 - Removable Pairings
-
- Book:
- Approximation Algorithms for Traveling Salesman Problems
- Published online:
- 14 November 2024
- Print publication:
- 05 December 2024, pp 265-279
-
- Chapter
- Export citation
18 - State of the Art, Open Problems
-
- Book:
- Approximation Algorithms for Traveling Salesman Problems
- Published online:
- 14 November 2024
- Print publication:
- 05 December 2024, pp 400-406
-
- Chapter
- Export citation
17 - Further Results, Related Problems
-
- Book:
- Approximation Algorithms for Traveling Salesman Problems
- Published online:
- 14 November 2024
- Print publication:
- 05 December 2024, pp 381-399
-
- Chapter
- Export citation
9 - Asymmetric Path TSP
-
- Book:
- Approximation Algorithms for Traveling Salesman Problems
- Published online:
- 14 November 2024
- Print publication:
- 05 December 2024, pp 183-211
-
- Chapter
- Export citation
14 - Symmetric Path TSP and T-Tours
-
- Book:
- Approximation Algorithms for Traveling Salesman Problems
- Published online:
- 14 November 2024
- Print publication:
- 05 December 2024, pp 303-323
-
- Chapter
- Export citation
3 - Linear Programming Relaxations of the Asymmetric TSP
-
- Book:
- Approximation Algorithms for Traveling Salesman Problems
- Published online:
- 14 November 2024
- Print publication:
- 05 December 2024, pp 47-65
-
- Chapter
- Export citation
2 - Linear Programming Relaxations of the Symmetric TSP
-
- Book:
- Approximation Algorithms for Traveling Salesman Problems
- Published online:
- 14 November 2024
- Print publication:
- 05 December 2024, pp 22-46
-
- Chapter
- Export citation
8 - Algorithms for Subtour Cover
-
- Book:
- Approximation Algorithms for Traveling Salesman Problems
- Published online:
- 14 November 2024
- Print publication:
- 05 December 2024, pp 159-182
-
- Chapter
- Export citation
4 - Duality, Cuts, and Uncrossing
-
- Book:
- Approximation Algorithms for Traveling Salesman Problems
- Published online:
- 14 November 2024
- Print publication:
- 05 December 2024, pp 66-86
-
- Chapter
- Export citation
15 - Best-of-Many Christofides and Variants
-
- Book:
- Approximation Algorithms for Traveling Salesman Problems
- Published online:
- 14 November 2024
- Print publication:
- 05 December 2024, pp 324-350
-
- Chapter
- Export citation
5 - Thin Trees and Random Trees
-
- Book:
- Approximation Algorithms for Traveling Salesman Problems
- Published online:
- 14 November 2024
- Print publication:
- 05 December 2024, pp 87-113
-
- Chapter
- Export citation
11 - Proving the Main Payment Theorem for Hierarchies
-
- Book:
- Approximation Algorithms for Traveling Salesman Problems
- Published online:
- 14 November 2024
- Print publication:
- 05 December 2024, pp 231-264
-
- Chapter
- Export citation
7 - Constant-Factor Approximation for the Asymmetric TSP
-
- Book:
- Approximation Algorithms for Traveling Salesman Problems
- Published online:
- 14 November 2024
- Print publication:
- 05 December 2024, pp 134-158
-
- Chapter
- Export citation
13 - Ear-Decompositions, Matchings, and Matroids
-
- Book:
- Approximation Algorithms for Traveling Salesman Problems
- Published online:
- 14 November 2024
- Print publication:
- 05 December 2024, pp 280-302
-
- Chapter
- Export citation
Ramsey simplicity of random graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 03 December 2024, pp. 298-320
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Optimal mixing via tensorization for random independent sets on arbitrary trees
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 26 November 2024, pp. 259-275
-
- Article
- Export citation
On the smallest gap in a sequence with Poisson pair correlations
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 21 November 2024, pp. 283-297
-
- Article
- Export citation
Long induced paths in expanders
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 19 November 2024, pp. 276-282
-
- Article
-
- You have access
- Open access
- HTML
- Export citation