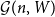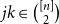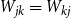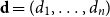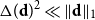Refine search
Actions for selected content:
6950 results in Algorithmics, Complexity, Computer Algebra, Computational Geometry
References
-
- Book:
- Data Structures and Algorithms in Java
- Published online:
- 19 December 2024
- Print publication:
- 31 October 2024, pp 604-609
-
- Chapter
- Export citation
12 - Project: Logic Puzzles
-
- Book:
- Data Structures and Algorithms in Java
- Published online:
- 19 December 2024
- Print publication:
- 31 October 2024, pp 362-381
-
- Chapter
- Export citation
5 - Searching and An Introduction to Algorithm Analysis
-
- Book:
- Data Structures and Algorithms in Java
- Published online:
- 19 December 2024
- Print publication:
- 31 October 2024, pp 154-177
-
- Chapter
- Export citation
Copyright page
-
- Book:
- Data Structures and Algorithms in Java
- Published online:
- 19 December 2024
- Print publication:
- 31 October 2024, pp vi-vi
-
- Chapter
- Export citation
10 - Sorting
-
- Book:
- Data Structures and Algorithms in Java
- Published online:
- 19 December 2024
- Print publication:
- 31 October 2024, pp 300-335
-
- Chapter
- Export citation
7 - Project: Particle Effects
-
- Book:
- Data Structures and Algorithms in Java
- Published online:
- 19 December 2024
- Print publication:
- 31 October 2024, pp 216-239
-
- Chapter
- Export citation
2 - Object-Oriented Programming
-
- Book:
- Data Structures and Algorithms in Java
- Published online:
- 19 December 2024
- Print publication:
- 31 October 2024, pp 57-90
-
- Chapter
- Export citation
13 - Queues and Buffers
-
- Book:
- Data Structures and Algorithms in Java
- Published online:
- 19 December 2024
- Print publication:
- 31 October 2024, pp 382-398
-
- Chapter
- Export citation
14 - Hashing
-
- Book:
- Data Structures and Algorithms in Java
- Published online:
- 19 December 2024
- Print publication:
- 31 October 2024, pp 399-418
-
- Chapter
- Export citation
Algorithms+Data Structures = Programs
-
- Book:
- Data Structures and Algorithms in Java
- Published online:
- 19 December 2024
- Print publication:
- 31 October 2024, pp 1-7
-
- Chapter
- Export citation
9 - Project: Generative Art and Fractals
-
- Book:
- Data Structures and Algorithms in Java
- Published online:
- 19 December 2024
- Print publication:
- 31 October 2024, pp 266-299
-
- Chapter
- Export citation
Index
-
- Book:
- Data Structures and Algorithms in Java
- Published online:
- 19 December 2024
- Print publication:
- 31 October 2024, pp 610-614
-
- Chapter
- Export citation
22 - Project: Twisty Little Passages
-
- Book:
- Data Structures and Algorithms in Java
- Published online:
- 19 December 2024
- Print publication:
- 31 October 2024, pp 581-603
-
- Chapter
- Export citation
Cokernel statistics for walk matrices of directed and weighted random graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 18 October 2024, pp. 131-150
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Embedding theorems for random graphs with specified degrees
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 16 October 2024, pp. 115-130
-
- Article
- Export citation
Sampling repulsive Gibbs point processes using random graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 11 October 2024, pp. 63-89
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Vertex-critical graphs far from edge-criticality
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 11 October 2024, pp. 151-157
-
- Article
-
- You have access
- Open access
- HTML
- Export citation

How to Think about Algorithms
-
- Published online:
- 10 October 2024
- Print publication:
- 07 March 2024
-
- Textbook
- Export citation
Approximation of subgraph counts in the uniform attachment model
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 10 October 2024, pp. 90-114
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A note on extremal constructions for the Erdős–Rademacher problem
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 10 October 2024, pp. 52-62
-
- Article
-
- You have access
- Open access
- HTML
- Export citation