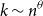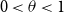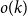Refine search
Actions for selected content:
6950 results in Algorithmics, Complexity, Computer Algebra, Computational Geometry
Noisy group testing via spatial coupling
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 19 November 2024, pp. 210-258
-
- Article
-
- You have access
- Open access
- HTML
- Export citation

Approximation Algorithms for Traveling Salesman Problems
-
- Published online:
- 14 November 2024
- Print publication:
- 05 December 2024
Expansion of the critical intensity for the random connection model
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 08 November 2024, pp. 158-209
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Reviews
-
- Book:
- Data Structures and Algorithms in Java
- Published online:
- 19 December 2024
- Print publication:
- 31 October 2024, pp ii-iv
-
- Chapter
- Export citation
1 - Java Fundamentals
-
- Book:
- Data Structures and Algorithms in Java
- Published online:
- 19 December 2024
- Print publication:
- 31 October 2024, pp 8-56
-
- Chapter
- Export citation
17 - Binary Trees
-
- Book:
- Data Structures and Algorithms in Java
- Published online:
- 19 December 2024
- Print publication:
- 31 October 2024, pp 455-487
-
- Chapter
- Export citation
19 - Heaps and Priority Queues
-
- Book:
- Data Structures and Algorithms in Java
- Published online:
- 19 December 2024
- Print publication:
- 31 October 2024, pp 517-537
-
- Chapter
- Export citation
Preface
-
- Book:
- Data Structures and Algorithms in Java
- Published online:
- 19 December 2024
- Print publication:
- 31 October 2024, pp xxiii-xxviii
-
- Chapter
- Export citation
3 - Project: Mindstorms
-
- Book:
- Data Structures and Algorithms in Java
- Published online:
- 19 December 2024
- Print publication:
- 31 October 2024, pp 91-111
-
- Chapter
- Export citation
16 - Project: Ye Olde Shakespearean Search Engine
-
- Book:
- Data Structures and Algorithms in Java
- Published online:
- 19 December 2024
- Print publication:
- 31 October 2024, pp 439-454
-
- Chapter
- Export citation
11 - Stacks
-
- Book:
- Data Structures and Algorithms in Java
- Published online:
- 19 December 2024
- Print publication:
- 31 October 2024, pp 336-361
-
- Chapter
- Export citation
Contents
-
- Book:
- Data Structures and Algorithms in Java
- Published online:
- 19 December 2024
- Print publication:
- 31 October 2024, pp ix-xxii
-
- Chapter
- Export citation
6 - Lists
-
- Book:
- Data Structures and Algorithms in Java
- Published online:
- 19 December 2024
- Print publication:
- 31 October 2024, pp 178-215
-
- Chapter
- Export citation
18 - Self-Balancing Search Trees
-
- Book:
- Data Structures and Algorithms in Java
- Published online:
- 19 December 2024
- Print publication:
- 31 October 2024, pp 488-516
-
- Chapter
- Export citation
4 - Arrays
-
- Book:
- Data Structures and Algorithms in Java
- Published online:
- 19 December 2024
- Print publication:
- 31 October 2024, pp 112-153
-
- Chapter
- Export citation
8 - Recursion
-
- Book:
- Data Structures and Algorithms in Java
- Published online:
- 19 December 2024
- Print publication:
- 31 October 2024, pp 240-265
-
- Chapter
- Export citation
21 - Project: Graph-Based Recommendation Engine
-
- Book:
- Data Structures and Algorithms in Java
- Published online:
- 19 December 2024
- Print publication:
- 31 October 2024, pp 566-580
-
- Chapter
- Export citation
Dedication
-
- Book:
- Data Structures and Algorithms in Java
- Published online:
- 19 December 2024
- Print publication:
- 31 October 2024, pp vii-viii
-
- Chapter
- Export citation
20 - Graph Algorithms
-
- Book:
- Data Structures and Algorithms in Java
- Published online:
- 19 December 2024
- Print publication:
- 31 October 2024, pp 538-565
-
- Chapter
- Export citation
15 - Hash Tables
-
- Book:
- Data Structures and Algorithms in Java
- Published online:
- 19 December 2024
- Print publication:
- 31 October 2024, pp 419-438
-
- Chapter
- Export citation