Refine search
Actions for selected content:
48274 results in Computer Science
10 - Broadcasts and Intelligent Machinery
-
- Book:
- Alan M. Turing
- Published online:
- 05 April 2012
- Print publication:
- 22 March 2012, pp 100-101
-
- Chapter
- Export citation
9 - Work with the Manchester Automatic Digital Machine
-
- Book:
- Alan M. Turing
- Published online:
- 05 April 2012
- Print publication:
- 22 March 2012, pp 88-99
-
- Chapter
- Export citation
9 - Network design and capacity
-
- Book:
- Understanding Weightless
- Published online:
- 05 April 2012
- Print publication:
- 22 March 2012, pp 130-146
-
- Chapter
- Export citation
7 - War Work in the Foreign Office
-
- Book:
- Alan M. Turing
- Published online:
- 05 April 2012
- Print publication:
- 22 March 2012, pp 67-76
-
- Chapter
- Export citation
Preface
-
- Book:
- Understanding Weightless
- Published online:
- 05 April 2012
- Print publication:
- 22 March 2012, pp xi-xi
-
- Chapter
- Export citation
5 - At the Graduate College, Princeton
-
- Book:
- Alan M. Turing
- Published online:
- 05 April 2012
- Print publication:
- 22 March 2012, pp 51-55
-
- Chapter
- Export citation
11 - Morphogenesis
-
- Book:
- Alan M. Turing
- Published online:
- 05 April 2012
- Print publication:
- 22 March 2012, pp 102-105
-
- Chapter
- Export citation
5 - Dynamic programming for action in the environment
-
- Book:
- Cognitive Dynamic Systems
- Published online:
- 05 June 2012
- Print publication:
- 22 March 2012, pp 125-166
-
- Chapter
- Export citation
Set Families With a Forbidden Induced Subposet
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 4 / July 2012
- Published online by Cambridge University Press:
- 22 March 2012, pp. 496-511
-
- Article
- Export citation
My Brother Alan
-
- Book:
- Alan M. Turing
- Published online:
- 05 April 2012
- Print publication:
- 22 March 2012, pp 145-166
-
- Chapter
- Export citation
Part Two - Concerning Computing Machinery and Morphogenesis
-
- Book:
- Alan M. Turing
- Published online:
- 05 April 2012
- Print publication:
- 22 March 2012, pp 123-124
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Cognitive Dynamic Systems
- Published online:
- 05 June 2012
- Print publication:
- 22 March 2012, pp i-iv
-
- Chapter
- Export citation
1 - Introduction
-
- Book:
- Cognitive Dynamic Systems
- Published online:
- 05 June 2012
- Print publication:
- 22 March 2012, pp 1-13
-
- Chapter
- Export citation
About the author
-
- Book:
- Understanding Weightless
- Published online:
- 05 April 2012
- Print publication:
- 22 March 2012, pp xiii-xiv
-
- Chapter
- Export citation
6 - The MAC layer
-
- Book:
- Understanding Weightless
- Published online:
- 05 April 2012
- Print publication:
- 22 March 2012, pp 74-101
-
- Chapter
- Export citation
8 - At the National Physical Laboratory, Teddington
-
- Book:
- Alan M. Turing
- Published online:
- 05 April 2012
- Print publication:
- 22 March 2012, pp 77-87
-
- Chapter
- Export citation
14 - Computing Machinery
-
- Book:
- Alan M. Turing
- Published online:
- 05 April 2012
- Print publication:
- 22 March 2012, pp 125-132
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Understanding Weightless
- Published online:
- 05 April 2012
- Print publication:
- 22 March 2012, pp i-iv
-
- Chapter
- Export citation
4 - At Cambridge
-
- Book:
- Alan M. Turing
- Published online:
- 05 April 2012
- Print publication:
- 22 March 2012, pp 40-50
-
- Chapter
- Export citation
Contents
-
- Book:
- Understanding Weightless
- Published online:
- 05 April 2012
- Print publication:
- 22 March 2012, pp v-x
-
- Chapter
- Export citation
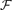
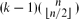 . This extends a result of Bukh [1], which in turn generalizes several known results including Sperner's theorem.
. This extends a result of Bukh [1], which in turn generalizes several known results including Sperner's theorem.