Refine search
Actions for selected content:
48585 results in Computer Science
Industrial Robots, Second Edition, Published by the Society of Manufacturing Engineers One SME Drive, Dearborn, Michigan 48121, USA (available in Europe exclusively from American Technical Publishers Ltd, 68a Wilbury Way, Hitchin, Herts, SG4 OTP, U.K.); 1985, 784 pp., index of participating companies (£35).
-
- Article
- Export citation
ROB volume 5 issue 4 Cover and Front matter
-
- Article
-
- You have access
- Export citation
ROB volume 11 issue 5 Back matter
-
- Article
-
- You have access
- Export citation
Special Announcement
-
- Article
-
- You have access
- Export citation
ROB volume 5 issue 4 Cover and Back matter
-
- Article
-
- You have access
- Export citation
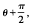 ,
,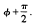 . Furthermore, a direction for carrying out such a translation can be determined in O(
. Furthermore, a direction for carrying out such a translation can be determined in O(